2015-2016学年河南省郑州市登封市高二下学期期中数学试卷(理科)
试卷更新日期:2017-03-23 类型:期中考试
一、选择题:
-
1. 计算: |x|dx=( )A、﹣1 B、1 C、﹣ D、2. 已知m∈R,i为虚数单位,则“m=1”是“复数z=m2﹣1+(m+1)i为纯虚数”的( )A、充分但不必要条件 B、必要但不充分条件 C、充要条件 D、既不充分也不必要条件3. 下面是一段“三段论”推理过程:设函数f(x)的导数为f′(x).若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点.因为f(x)=x3在(﹣1,1)内无极值点,所以f′(x)=3x2在(﹣1,1)内无零点.以上推理中( )A、大前提错误 B、小前提错误 C、结论正确 D、推理形式错误4. 已知i为虚数单位,复数z满足 =i,则z2016=( )A、﹣2i B、2i C、﹣1 D、15. 由直线y=0,x=e,y=2x及曲线 所围成的封闭的图形的面积为( )A、3+2ln2 B、3 C、2e2﹣3 D、e6. 如果命题p(n)对n=k成立,则它对n=k+2也成立,若p(n)对n=2成立,则下列结论正确的是( )A、p(n)对所有正整数n都成立 B、p(n)对所有正偶数n都成立 C、p(n)对大于或等于2的正整数n都成立 D、p(n)对所有自然数都成立7. 小赵、小钱、小孙、小李四位同学被问到谁去过长城时,
小赵说:我没去过;
小钱说:小李去过;
小孙说;小钱去过;
小李说:我没去过.
假定四人中只有一人说的是假话,由此可判断一定去过长城的是( )
A、小赵 B、小李 C、小孙 D、小钱8. 把一个带+q电量的点电荷放在r轴上原点处,形成一个电场,距离原点为r处的单位电荷受到的电场力由公式F=k (其中k为常数)确定,在该电场中,一个单位正电荷在电场力的作用下,沿着r轴的方向从r=a处移动到r=2a处,与从r=2a处移动到r=3a处,电场力对它所做的功之比为( )A、 B、 C、 D、39. 给出下列4个求导运算,其中正确的个数是( )①(x+ )′=1+ ;
②(log2x)′= ;
③(3x)′=3x•log3e;
④(x2cos2x)′=﹣2xsin2x.
A、1 B、2 C、3 D、410. 用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )A、假设三内角都不大于60度 B、假设三内角都大于60度 C、假设三内角至多有一个大于60度 D、假设三内角至多有两个大于60度11. 设函数f(x)在R上可导,其导函数f′(x),且函数f(x)在x=﹣2处取得极小值,则函数y=xf′(x)的图象可能是( )A、 B、
B、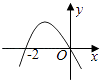 C、
C、 D、
D、 12. 已知函数f(x)= x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )A、 B、 C、 D、
12. 已知函数f(x)= x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )A、 B、 C、 D、二、填空题:
-
13. 已知函数f(x)= ﹣ +x+d在R上单调,则b的取值范围为 . (用区间表示)14. 若复数z满足3z+ =1+i,其中i是虚数单位,则z= .15. 在圆中有“圆心与弦(非直径)的中点的连线垂直于弦所在的直线”.比上述性质,相应地:在球中有 .16. 设a>1,若关于x的方程ax=x无实根,则实数a的取值范围为 . (用区间表示)
三、解答题:
-
17. 已知函数f(x)=x2﹣3x+alnx(a>0).
(Ⅰ)若a=1,求函数f(x)的单调区间和极值;
(Ⅱ)设函数f(x)图象上任意一点的切线l的斜率为k,当k的最小值为1时,求此时切线l的方程.
18. 数列{an}满足a1=1,an+1= (n∈N*).(1)、计算a2 , a3 , a4 , 并由此猜想通项公式an;(2)、用数学归纳法证明(1)中的猜想.19. 已知复数z在复平面内对应的点在第四象限,且z是方程x2﹣4x+5=0的根.(1)、求复数z;(2)、复数w=a﹣ (a∈R)满足|w﹣z|<2 ,求a的取值范围.20. 某商店商品每件成本10元,若售价为25元,则每天能卖出288件,经调查,如果降低价格,销售量可以增加,且每天多卖出的商品件数t与商品单价的降低值x(单位:元,0≤x≤15)的关系是t=6x2 .(1)、将每天的商品销售利润y表示成x的函数;(2)、如何定价才能使每天的商品销售利润最大?