2019河北省中考数学模拟试卷
试卷更新日期:2018-11-22 类型:中考模拟
一、单选题
-
1. 下面是小明用三根火柴组成的图形,其中符合三角形概念的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知:岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则符合条件的示意图是( )A、
2. 已知:岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则符合条件的示意图是( )A、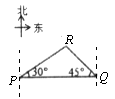 B、
B、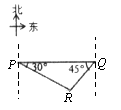 C、
C、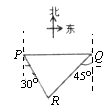 D、
D、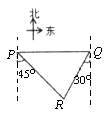 3. 如果m2+2m﹣2=0,那么代数式(m+ )• 的值是( )A、﹣2 B、﹣1 C、2 D、34. 近年来,国家重视精准扶贫,收效显著.据统计约有65 000 000人脱贫,把65 000 000用科学记数法表示,正确的是( )A、0.65×108 B、6.5×107 C、6.5×108 D、65×1065. 如图,线段AB上有C、D两点,以AC,CD,BD为直径的圆的周长分别为C1、C2、C3 , 以AB为直径的圆的周长为C,下列结论正确的是( )
3. 如果m2+2m﹣2=0,那么代数式(m+ )• 的值是( )A、﹣2 B、﹣1 C、2 D、34. 近年来,国家重视精准扶贫,收效显著.据统计约有65 000 000人脱贫,把65 000 000用科学记数法表示,正确的是( )A、0.65×108 B、6.5×107 C、6.5×108 D、65×1065. 如图,线段AB上有C、D两点,以AC,CD,BD为直径的圆的周长分别为C1、C2、C3 , 以AB为直径的圆的周长为C,下列结论正确的是( )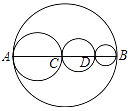 A、C1+C2=C+C3 B、C1+C2+C3=C C、C1+C2+C3>C D、C1+C2+C3<C6. 小明在抄分解因式的题目时,不小心漏抄了x的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数),则这个指数可能的结果共有( )
A、C1+C2=C+C3 B、C1+C2+C3=C C、C1+C2+C3>C D、C1+C2+C3<C6. 小明在抄分解因式的题目时,不小心漏抄了x的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数),则这个指数可能的结果共有( )
A、2种 B、3种 C、4种 D、5种7. 下列说法:①在等式2x=4两边都加上2,可得等式4x=6;②在等式2x=4两边都减去2,可得等式x=2;③在等式2x=4两边都乘以 ,等式变为x=2;④等式两边都除以同一个数,等式仍然成立.其中正确的说法有( )
A、1个 B、2个 C、3个 D、4个8. 小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个 不透明的箱子中装有红、黄、白三种球各 1 个,这些球除颜色外无其他差别,从箱子中随机摸出 1 个球,然后放回箱子中轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( )A、 B、 C、 D、9. 一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )
10. 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )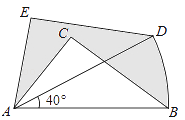 A、 π﹣6 B、 π C、 π﹣3 D、 +π11. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )
A、 π﹣6 B、 π C、 π﹣3 D、 +π11. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )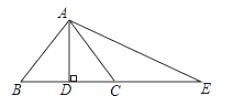 A、AB>AC=CE B、AB=AC>CE C、AB>AC>CE D、AB=AC=CE12. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
A、AB>AC=CE B、AB=AC>CE C、AB>AC>CE D、AB=AC=CE12. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 13.
13.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是( )
 A、点A B、点B C、点C D、点D14. 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形(如图).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A、点A B、点B C、点C D、点D14. 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形(如图).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )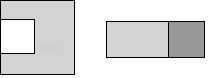 A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣ab=a(a﹣b)15. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣ab=a(a﹣b)15. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、 B、
B、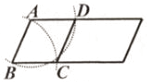 C、
C、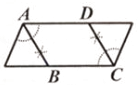 D、
D、 16. 抛物线 的部分图象如图所示,与x轴的一个交点坐标为 ,抛物线的对称轴是 下列结论中:
16. 抛物线 的部分图象如图所示,与x轴的一个交点坐标为 ,抛物线的对称轴是 下列结论中:; ; 方程 有两个不相等的实数根; 抛物线与x轴的另一个交点坐标为 ; 若点 在该抛物线上,则 .
其中正确的有
 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
17. 若式子 在实数范围内有意义,则 的取值范围是 .18. 已知am=3,an=2,则a2m﹣n的值为 .
19. 如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1 , 若图中阴影部分的三角形都是等腰直角三角形,则从左往右第4个阴影三角形的面积是 , 第2017个阴影三角形的面积是 .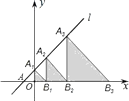
三、解答题
-
20. 有这样一道题:“计算 的值,其中 ”甲同学把“ ”错抄成了“ ”但他计算的结果也是正确的,请你通过计算说明为什么?
21. 某中学对本校500名毕业生中考体育加试测试情况进行调查,根据男生1 000m及女生800m测试成绩整理、绘制成如下不完整的统计图(图①、图②),请根据统计图提供的信息,回答下列问题: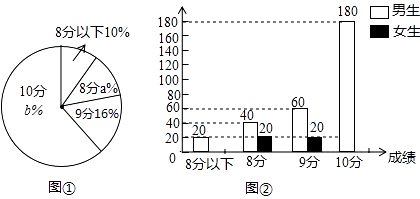 (1)、该校毕业生中男生有人,女生有人;(2)、扇形统计图中a= , b=;(3)、补全条形统计图(不必写出计算过程).22. 某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?
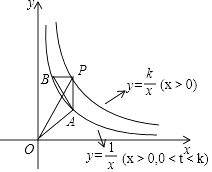
(1)、该校毕业生中男生有人,女生有人;(2)、扇形统计图中a= , b=;(3)、补全条形统计图(不必写出计算过程).22. 某小区有一块长21米,宽8米的矩形空地,如图所示.社区计划在其中修建两块完全相同的矩形绿地,并且两块绿地之间及四周都留有宽度为x米的人行通道.如果这两块绿地的面积之和为60平方米,人行通道的宽度应是多少米?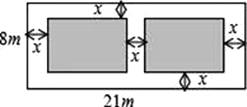 23. 如图所示,Rt△PAB的直角顶点P(3,4)在函数y= (x>0)的图象上,顶点A、B在函数y= (x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB .
23. 如图所示,Rt△PAB的直角顶点P(3,4)在函数y= (x>0)的图象上,顶点A、B在函数y= (x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB .①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin .
 24. 在平面直角坐标系中,O为原点,点A(1,0),点B(0, ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
24. 在平面直角坐标系中,O为原点,点A(1,0),点B(0, ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
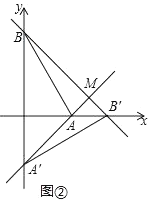
(Ⅰ)如图①,当α=30°时,求点B′的坐标;
(Ⅱ)设直线AA′与直线BB′相交于点M.
如图②,当α=90°时,求点M的坐标;
②点C(﹣1,0),求线段CM长度的最小值.(直接写出结果即可)
25. 如图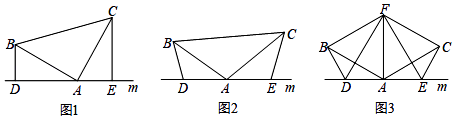 (1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.26. 如图,平面直角坐标系xOy中,抛物线y=a(x+1)(x-9)经过A,B两点,四边形OABC矩形,已知点A坐标为(0,6)。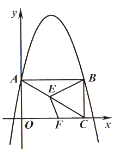 (1)、求抛物线解析式;(2)、点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断 的值是否变化;若不变,求出它的值;若变化,请说明理由。(3)、在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点E在抛物线对称轴上时,请求出BE的长度。
(1)、求抛物线解析式;(2)、点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断 的值是否变化;若不变,求出它的值;若变化,请说明理由。(3)、在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点E在抛物线对称轴上时,请求出BE的长度。