2015-2016学年福建省福州市五校联考高二下学期期中数学试卷(理科)
试卷更新日期:2017-03-23 类型:期中考试
一、选择题
-
1. ﹣ xdx=( )A、- B、 C、﹣1 D、12. 复数 (i为虚数单位)的共轭复数是( )A、 B、 C、 D、3. 一个物体的运动方程为s=1﹣t+t2其中s的单位是米,t的单位是秒,那么物体在t=4时的瞬时速度是( )A、7米/秒 B、6米/秒 C、5米/秒 D、8米/秒4. 若曲线f(x)=x4﹣4x在点A处的切线平行于x轴,则点A的坐标为( )A、(﹣1,2) B、(1,﹣3) C、(1,0) D、(1,5)5. 下面几种推理过程是演绎推理的是( )A、由平面三角形的性质推测空间三棱锥的性质 B、所有的金属都能够导电,铀是金属,所以铀能够导电 C、高一参加军训有12个班,1班51人,2班53人,三班52人,由此推测各班都超过50人 D、在数列{an}中,a1=2,an=2an﹣1+1(n≥2),由此归纳出{an}的通项公式6. 电动自行车的耗电量y与速度x的关系为y= ﹣40x(x>0),为使耗电量最小,则速度应为( )A、45 B、40 C、35 D、307. 若函数y=x3﹣3bx+1在区间(1,2)内是减函数,b∈R,则( )A、b≤4 B、b<4 C、b≥4 D、b>48. 下列求导运算正确的是( )A、( )′=x B、(x•ex)′=ex+1 C、(x2cosx)′=﹣2xsinx D、9. 函数g(x)=﹣x2+2lnx的图象大致是( )A、
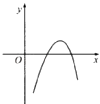 B、
B、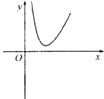 C、
C、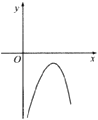 D、
D、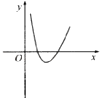 10. 用数学归纳法证明“ ”时,由n=k的假设证明n=k+1时,如果从等式左边证明右边,则必须证得右边为( )A、 B、 C、 D、11. 如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )
10. 用数学归纳法证明“ ”时,由n=k的假设证明n=k+1时,如果从等式左边证明右边,则必须证得右边为( )A、 B、 C、 D、11. 如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )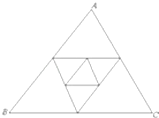 A、 B、 C、 D、212. 已知奇函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x>0时有2f(x)+xf′(x)>x2 , 则不等式(x+2014)2f(x+2014)+4f(﹣2)<0的解集为( )A、(﹣∞,﹣2012) B、(﹣2016,﹣2012) C、(﹣∞,﹣2016) D、(﹣2016,0)
A、 B、 C、 D、212. 已知奇函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x>0时有2f(x)+xf′(x)>x2 , 则不等式(x+2014)2f(x+2014)+4f(﹣2)<0的解集为( )A、(﹣∞,﹣2012) B、(﹣2016,﹣2012) C、(﹣∞,﹣2016) D、(﹣2016,0)二、填空题
-
13. 曲线y= 和直线y=x围成的图形面积是 .14. 用反证法证明命题:“设实数a,b,c满足a+b+c=3,则a,b,c中至少有一个数不小于1”时,第一步应写:假设 .15. 已知f(x)=x2+3xf′(2),则1+f′(1)= .16. 下列命题中正确的有 . (填上所有正确命题的序号)
①一质点在直线上以速度v=3t2﹣2t﹣1(m/s)运动,从时刻t=0(s)到t=3(s)时质点运动的路程为15(m);
②若x∈(0,π),则sinx<x;
③若f′(x0)=0,则函数y=f(x)在x=x0取得极值;
④已知函数 ,则 .
三、解答题
-
17. 用分析法证明:当x≥4时, + > + .18. 设z1=2x+1+(x2﹣3x+2)i,z2=x2﹣2+(x2+x﹣6)i(x∈R).(1)、若z1是纯虚数,求实数x的取值范围;(2)、若z1>z2 , 求实数x的取值范围.19. 已知函数f(x)= ﹣ax+b,在点M(1,f(1))处的切线方程为9x+3y﹣10=0,求(1)、实数a,b的值;(2)、函数f(x)的单调区间以及在区间[0,3]上的最值.20. 已知a1= (n∈N*)(1)、求a2 , a3 , a4并由此猜想数列{an}的通项公式an的表达式;(2)、用数学归纳法证明你的猜想.