沪科版八年级数学上册 第十三章单元检测b卷

试卷更新日期：2018-11-21 类型：单元试卷

进入 出卷网 下载

一、选择题

  • 1. 如图所示，AB⊥EF，CD⊥EF，∠1=∠F=45°，那么与∠FCD（不包括∠FCD）相等的角有（ ）

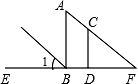    A、5个 B、2个 C、3个 D、4个

    查看试题解析

  • 2. 在△ABC中，∠A，∠B，∠C的度数之比为2：3：4，则∠B的度数为（   ）
    A、120° B、80° C、60° D、40°

    查看试题解析

  • 3. 下列说法正确的是（  ）

    ①三角形的角平分线是射线；

    ②三角形的三条角平分线都在三角形内部，且交于同一点；

    ③三角形的三条高都在三角形内部；

    ④三角形的一条中线把该三角形分成面积相等的两部分．

    A、①② B、②③ C、③④ D、②④

    查看试题解析

  • 4. 如图，直线l1 ∥ l2 ， CD⊥AB于点D ，∠1=50°，则∠BCD的度数为（   ）

    A、40° B、45° C、50° D、30°

    查看试题解析

  • 5. 小桐把一副直角三角尺按如图所示的方式摆放在一起，其中 ∠E=90° ， ∠C=90° ， ∠A=45° ， ∠D=30° ，则 ∠1+∠2 等于（   ）

    A、150° B、180° C、210° D、270°

    查看试题解析

  • 6.

    如图，直线l1∥l2 ， ∠1=50°，∠2=23°20′，则∠3的度数为（　　）

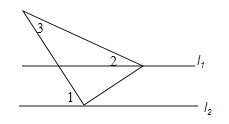    A、26°40′   B、27°20′ C、27°40′ D、73°20′

    查看试题解析

  • 7. 如图，在△ABC中，∠A=60度，点D，E分别在AB，AC上，则∠1+∠2的大小为（   ）度.

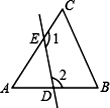    A、140 B、190 C、320 D、240

    查看试题解析

  • 8. 如图，△ABC中，∠ABC，∠ACB的三等分线交于点E，D，若∠BFC=120°，∠BGC=102°，则∠A的度数为（   ）

    A、34° B、40° C、42° D、46°

    查看试题解析

  • 9. 如图有四条互相不平行的直线l1、l2、l3、l4所截出的七个角，关于这七个角的度数关系，下列结论正确的是（   ）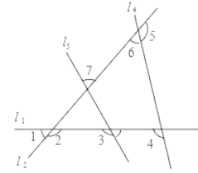


    A、∠2=∠4+∠7 B、∠3=∠1+∠7 C、∠1+∠4+∠6=180° D、∠2+∠3+∠5=360°

    查看试题解析

  • 10. △ABC中，已知点D，E，F 分别是BC，AD，CE边上的中点，且S△ABC=4cm2 ， 则S△BEF的值为（    ）

    A、2cm2 B、1cm2 C、0.5cm2 D、0.25cm2

    查看试题解析

  • 11. 如图，已知直线AB∥CD，∠C=135°，∠A=45°，则△AEF的形状是（   ）

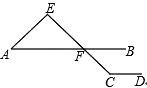    A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

    查看试题解析

二、填空题

  • 12. 若要与长为4、7的两根木条组成三角形，那么第三条木棍x取值范围应为。

    查看试题解析

  • 13. 已知a，b，c是△ABC的三边长，a，b满足|a﹣7|+（b﹣1）2=0，c为奇数，则c= ．

    查看试题解析

  • 14. 若△ABC三条边长为a，b，c，化简：|a-b-c|-|a+c-b|= ．

    查看试题解析

  • 15. 一副分别含有30°和45°的两个直角三角板，拼成如图图形，其中∠C=90°，∠B=45°，∠E=30°．则∠BFD的度数是 ．

    查看试题解析

  • 16. 如图，△ABC中，点E是BC上的一点，EC=2BE，BD是边AC上的中线，若S△ABC=18，则S△ADF-S△BEF= ．

    查看试题解析

  • 17. 如图，在△ABC中，∠ABC的平分线与∠ACD的平分线交于点A1 ， ∠A1BC的平分线与∠A1CD的平分线交于点A2 ， 依此类推…．已知∠A=α，则∠An的度数为（用含n、α的代数式表示）．

    查看试题解析

三、解答题

  • 18. 已知a，b，c是三角形的三边长．
    (1)、化简：|a-b-c|+|b-c-a|+|c-a-b|；
    (2)、在（1）的条件下，若a=5，b=4，c=3，求这个式子的值．

    查看试题解析

  • 19. 如图，在 △ABC 中，∠A=30°，∠B=70°，CE⊥AB，垂足为 E ， CF 平分∠ACE，求∠FCE的度数．

    查看试题解析

  • 20. 如图，AD是△ABC的角平分线，∠B=50°，∠ADC=70°，求∠BAC、∠C的度数．

    查看试题解析

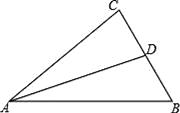  • 21. 如图，在△ABC中，∠BAC=75°，AD、BE分别是BC、AC边上的高，AD=BD，求∠C和∠AFB的度数.

    查看试题解析

  • 22. 已知：如图， P 是 △ABC 内一点．求证： AB+AC>PB+PC ．

    查看试题解析

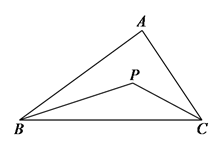  • 23. 在△ABC中，点D在边BA或BA的延长线上，过点D作DE∥BC，交∠ABC的角平分线于点E．

    (1)、如图1，当点D在边BA上时，点E恰好在边AC上，求证：∠ADE=2∠DEB；
    (2)、如图2，当点D在BA的延长线上时，请直接写出∠ADE与∠DEB之间的数量关系，并说明理由．

    查看试题解析

  • 24. 在△ABC中，∠C＞∠B，AE平分∠BAC，F为射线AE上一点（不与点E重合），且FD⊥BC于D；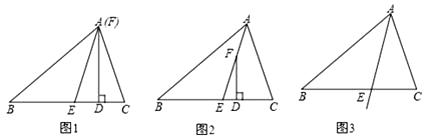

    (1)、如果点F与点A重合，且∠C=50°，∠B=30°，如图1，求∠EFD的度数；
    (2)、如果点F在线段AE上（不与点A重合），如图2，问∠EFD与∠C﹣∠B有怎样的数量关系？并说明理由．
    (3)、如果点F在△ABC外部，如图3，此时∠EFD与∠C﹣∠B的数量关系是否会发生变化？请说明理由．

    查看试题解析

  • 25. 如图（a），∠DAB+∠ABC+∠BCE=360°

    (1)、求证：AD∥CE
    (2)、如图（b），AG、CG分别平分∠BAD、∠BCE，BF∥AG交GC的延长线于F，判断∠ABC与∠F的数量关系，并证明；
    (3)、如图（c），AN平分∠HAB，BP平分∠ABC，BQ∥AN，CM平分∠BCT交BQ的反向延长线于M，① ∠QBP∠ABC 的值不变，② ∠QMC∠ABC 的值不变；其中只有一个结论正确，请择一证明．

    查看试题解析