沪科版八年级数学上册 13.2命题与证明 同步练习（三）
试卷更新日期：2018-11-21 类型：同步测试
一、选择题
-
1. 如图，l∥m，∠1=115°，∠2=95°，则∠3=（ ）
A、120° B、130° C、140° D、150°2. 如图，△ABC中，∠A=46°，∠C=74°，BD平分∠ABC，交AC于点D，那么∠BDC的度数是（ ）
A、76° B、81° C、92° D、104°3. 如图，点D在△ABC的边AB的延长线上，DE∥BC，若∠A＝35°，∠C＝24°，则∠D的度数是（ ）。
A、24° B、59° C、60° D、69°4. 如图，已知a∥b，∠1=130°，∠2=90°，则∠3=（ ）
A、70° B、100° C、140° D、170°5. 如图2，已知AB∥CD，∠C=70°，∠F=30°，则∠A的度数为（ ）
A、30° B、35° C、40° D、45°6. 如图，已知矩形纸片的一条边经过一个含30°角的直角三角尺的直角顶点，若矩形纸片的一组对边分别与直角三角尺的两边相交，∠2=115°，则∠1的度数是（ ）
A、75° B、85° C、60° D、65°7. 含30°角的直角三角板与直线l1、l2的位置关系如图所示，已知l1∥l2 ， ∠ACD=∠A，则∠1=（ ）
A、70° B、60° C、40° D、30°8. 如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，那么下列式子中正确的是（ ）
A、γ=2α+β B、γ=α+2β C、γ=α+β D、γ=180°﹣α﹣β二、填空题
-
9. 如图，在△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=25°，则∠ADE=°．
10. 如图，△ABC中，∠A=100°，若BM、CM分别是△ABC的外角平分线，则∠M= ．
11. 如图，在△ABC中，AB=AD=DC，∠BAD=20°，则∠C= ．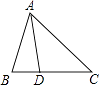
12. 如图，在△ABC中，BD平分∠ABC，CE平分∠ACB，BD与CE交于点M.若MN⊥BC于N，∠A＝60°，则∠1－∠2=度.
13. 如图，AB∥CD，CP交AB于点O，AO=PO，若∠A=35°，则∠C=°．
14. 如图，点D，B，C在同一直线上，∠A＝60°，∠C＝50°，∠D＝25°，则∠1＝.
15. 如图，∠B＝46°，△ABC的外角∠DAC和∠ACF的平分线交于点E，则∠AEC的度数为 ．
三、解答题
-
16. 如图，△ABC中，∠A=80°，∠B、∠C的角平分线相交于点O，∠ACD=30°，求∠DOB的度数.
17. 如图，在△ABC中，D是AB上一点，E是AC上一点，BE与CD相交于点O，∠A=60°，∠ABE=15°，∠ACD=25°，求∠COE的度数．
18. 如果，在△ABC中，AD是高，AE是∠BAC的平分线，∠BAC=54°，∠C=70°．求∠EAD的度数．
19. 一天，爸爸带着小刚到建筑工地去玩，看见有如图所示的人字架，爸爸说“小刚，我考考你，这个人字架的夹角∠1等于130°，你能求出∠3比∠2大多少吗？”小刚马上得到了正确答案，他的答案是多少？请说明理由．
20. 已知：△ABC中，记∠BAC=α，∠ACB=β．
(1)、如图1，若AP平分∠BAC，BP，CP分别平分△ABC的外角∠CBM和∠BCN，BD⊥AP于点D，用α的代数式表示∠BPC的度数，用β的代数式表示∠PBD的度数.
(2)、如图2，若点P为△ABC的三条内角平分线的交点，BD⊥AP于点D，猜想（1）中的两个结论是否发生变化，补全图形并直接写出你的结论．21. 如图，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点．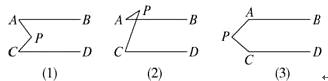
(1)、当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．(2)、当点P移动到AB的外侧时，如图（2），是否仍有（1）的结论？如果不是，请写出你的猜想（不要求证明）．
(3)、当点P移动到如图（3）的位置时，∠P与∠A、∠C又有怎样的关系？能否利用（1）的结论来证明？还有其他的方法吗？请写出一种．