沪科版八年级数学上册 13.2命题与证明 同步练习（二）
试卷更新日期：2018-11-21 类型：同步测试
一、选择题
-
1. 如图，a∥b，以直线b上两点A和B为顶点的Rt△ABC（其中∠C=90°）与直线a相交，若∠1=30°，则∠ABC的度数为（ ）
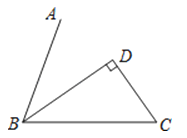
A、30° B、60° C、120° D、150°2.如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（ ）
A、35° B、55° C、60° D、70°3. 如图，直线l1 ∥ l2 ， CD⊥AB于点D ，∠1=50°，则∠BCD的度数为（ ）
A、40° B、45° C、50° D、30°4. 如图，直线 ，直线l与a，b分别交于点A，B，过点A作AC⊥b 于点C，若∠1=50°，则∠2的度数为（ ）
A、 B、 C、 D、5. 已知直线a∥b，将一块含30°的直角三角尺按如图方式放置（∠ABC=60°），其中A，C两点分别落在直线a，b上，若∠1=20°，则∠2的度数为（ ）
A、20° B、30° C、40° D、50°6. 在△ABC中，已知∠ABC=66°，∠ACB=54°，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，∠EHF的度数是（ ）
A、50° B、40° C、130° D、120°7. 如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
A、135° B、150° C、270° D、90°8. 如图，△ABC的角平分线CD、BE相交于F，∠A=90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG=2∠DCB；②∠DFB= ∠CGE；③∠ADC=∠GCD；④CA平分∠BCG．
其中正确的个数是（ ）
A、1 B、2 C、3 D、4二、填空题
-
9. 如图示在△ABC中∠B= ．
10. 过△ABC的顶点C作AB的垂线，如果该垂线将∠ACB分为40°和20°的两个角，那么∠A，∠B中较大的角的度数是 ．11. 如图，已知∠AON=40°，OA=6，点P是射线ON上一动点，当△AOP为直角三角形时，∠A=.
12. 若直角三角形的两个锐角之差为34°，则此三角形较小锐角的度数为 ．13. 把一块直尺与一块三角板如图放置，若∠1=60°，则∠2=°．
14. 如图，将一副三角板叠放在一起，则图中∠α的度数是度．
15. 如图，BC⊥ED于点O，∠A=50°，∠D=20°，则∠B=度．
三、解答题
-
16. 已知 中， ， BD是AC边上的高，AE平分 ， 分别交BC、BD于点E、F，求证： ．
17. 如图，在Rt△ABC中，∠BAC=90°，AD是BC边上的中线，ED⊥BC于D，交BA延长线于点E，若∠E=35°，求∠BDA的度数．
18. 如图，在△ABC中，CD是△ABC的高线，CE是△ABC的角平分线，已知 ∠B=30° ，∠DCE=15°．试判断△ABC的形状，并证明你的判断．
