沪科版八年级数学上册 13.1三角形中的边角关系 同步练习(三)
试卷更新日期:2018-11-21 类型:同步测试
一、选择题
-
1. 下面四个图形中,线段BE是△ABC的高的图是( )A、
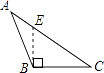 B、
B、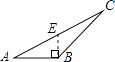 C、
C、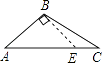 D、
D、 2. 如图所示,△ABC中AB边上的高线是( )
2. 如图所示,△ABC中AB边上的高线是( )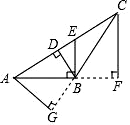 A、线段AG B、线段BD C、线段BE D、线段CF3. 如图,AD是△ABC的中线,已知△ABD比△ACD的周长长6cm,则AB与AC的差为( )
A、线段AG B、线段BD C、线段BE D、线段CF3. 如图,AD是△ABC的中线,已知△ABD比△ACD的周长长6cm,则AB与AC的差为( ) A、2cm B、3cm C、6cm D、12cm4. 如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( )
A、2cm B、3cm C、6cm D、12cm4. 如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( )①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
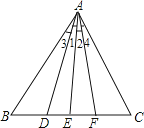 A、4个 B、3个 C、2个 D、1个5. 如图所示,AB⊥AD,AB⊥BC,则以AB为一条高线的三角形共有( )
A、4个 B、3个 C、2个 D、1个5. 如图所示,AB⊥AD,AB⊥BC,则以AB为一条高线的三角形共有( )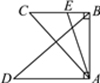 A、1个 B、2个 C、3个 D、4个6. 如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( )
A、1个 B、2个 C、3个 D、4个6. 如图,AD⊥BC于D,DE是△ADC的中线,则以AD为高的三角形有( ) A、3 个 B、4 个 C、5 个 D、6 个7. 如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,点D到AB的距离是( )
A、3 个 B、4 个 C、5 个 D、6 个7. 如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,点D到AB的距离是( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
8. 在三角形的中线,高线,角平分线中,一定能把三角形的面积等分的是.9. BM是△ABC中AC边上的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长之差为cm.10. 如图,△ABC中,点D、E分别是BC、AD的中点,△ABC的面积为6,则阴影部分的面积是 .
 11. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B= .
11. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B= . 12. 如图所示,阴影部分的面积是 , , ,则 的面积是 .
12. 如图所示,阴影部分的面积是 , , ,则 的面积是 . 13. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为 .
13. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为 .
三、解答题
-
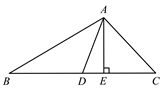
14. 如图,△ABC中,AD、AE分别是边BC上的中线和高,AE=4,S△ABD=10,求BC,CD的长.
 15. 如图,在 中, ,求 的长.
15. 如图,在 中, ,求 的长. 16. 如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
16. 如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.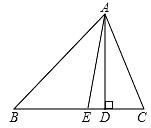 (1)、求∠BAE的度数;(2)、求∠DAE的度数.17. 有一块三角形优良品种试验基地,如图,由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制订出两种以上的划分方案以供选择(画图说明).
(1)、求∠BAE的度数;(2)、求∠DAE的度数.17. 有一块三角形优良品种试验基地,如图,由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制订出两种以上的划分方案以供选择(画图说明). 18. 如图,在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
18. 如图,在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.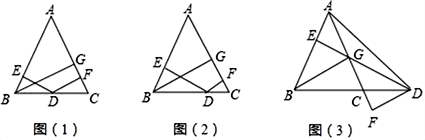 (1)、在图(1)中,D是BC边上的中点,判断DE+DF和BG的关系,并说明理由.(2)、在图(2)中,D是线段BC上的任意一点,DE+DF和BG的关系是否仍然成立?如果成立,证明你的结论;如果不成立,请说明理由.(3)、在图(3)中,D是线段BC延长线上的点,探究DE、DF与BG的关系.(不要求证明,直接写出结果)19. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.
(1)、在图(1)中,D是BC边上的中点,判断DE+DF和BG的关系,并说明理由.(2)、在图(2)中,D是线段BC上的任意一点,DE+DF和BG的关系是否仍然成立?如果成立,证明你的结论;如果不成立,请说明理由.(3)、在图(3)中,D是线段BC延长线上的点,探究DE、DF与BG的关系.(不要求证明,直接写出结果)19. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.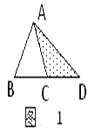

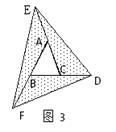

(1)、如图1,延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1 , 则S1=(用含a的代数式表示);
(2)、如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2 , 则S2=(用含a的代数式表示);(3)、在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3 , 则S3=(用含a的代数式表示).发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的倍.