沪科版八年级数学上册 13.1三角形中的边角关系 同步练习（二）
试卷更新日期：2018-11-21 类型：同步测试
一、选择题
-
1. ABC中，∠A∶∠B∶∠C=3∶4∶5，则∠C等于（ ）A、45° B、60° C、75° D、90°2. 如图，△ABC中，∠A=60°，∠B=40°，则∠C等于（ ）
A、100° B、80° C、60° D、40°3.△ABC中，BF、CF是角平分线，∠A=70°，则∠BFC=（ ）
A、125° B、110° C、100° D、150°4. 如图，AB∥CD，且∠DEC=100°，∠C=40°，则∠B的大小是（ ）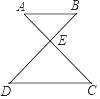
A、30° B、40° C、50° D、60°5. 如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，∠BAC=60°，∠ABE=25°，则∠DAC的大小是（ ）
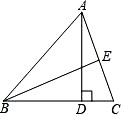A、15° B、20° C、25° D、30°6. 一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（ ）
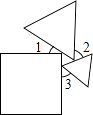A、90° B、100° C、130° D、180°7. 如图，AB∥CD，∠BED=61°，∠ABE的平分线与∠CDE的平分线交于点F，则∠DFB=（ ）
A、149° B、149.5° C、150° D、150.5°二、填空题
-
8. 将一副三角板如图叠放，则图中∠α的度数为 ．
9. 在△ABC中，若∠A=30°，∠B=50°，则∠C= ．10. 在△ABC中，∠ABC和∠ACB的平分线交于点I，若∠A=60°，则∠BIC= ．11. 如图，AD是△ABC的高，BE是△ABC的内角平分线，BE、AD相交于点F，已知∠BAD=40°，则∠BFD=°．
12. 如图，在△ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，则∠DBC=度．
13. 如图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A= ．
三、解答题
-
14. 如图，在△ABC中，∠A=70°，∠B=50°，CD平分∠ACB，求∠ACD的度数．
15. 如图，已知∠A=∠1，∠C=∠F，请问BC与EF平行吗？请说明理由．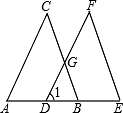
16. 在△ABC中，∠B=∠C，且∠A与∠B的比例为1：a，用代数式表示A，B，C的度数．17. 在△ABC中，BO、CO分别平分∠CBA、∠BCA，求证：∠COB= ∠CAB+90°．
18. 如图1，AB与CD相交于点O，若∠D=38°，∠B=28°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试求：
(1)、∠P的度数；(2)、设∠D=α，∠B=β，∠DAP= ∠DAB，∠DCP= ∠DCB，其他条件不变，如图2，试问∠P与∠D、∠B之间存在着怎样的数量关系（用α、β表示∠P），直接写出结论．19. 平面内的两条直线有相交和平行两种位置关系
(1)、如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B﹣∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；(2)、在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）(3)、根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．