浙江省余姚市2017-2018学年七年级上学期数学期中考试试卷
试卷更新日期:2018-11-21 类型:期中考试
一、单选题
-
1. 3的倒数是( )A、 B、 C、3 D、-32. 计算:(-8)+(+5)=( )A、3 B、-3 C、13 D、-133. 下面给出的四条数轴中画得正确的是( )A、
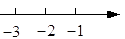 B、
B、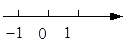 C、
C、 D、
D、 4. 今年余姚市上半年接待国内外游客650多万人次,实现旅游总收入61亿元,其中,61亿用科学记数法表示是( )A、 B、 C、 D、5. 按要求对0.05019分别取近似值,下面结果错误的是( )A、0.1(精确到0.1) B、0.05(精确到0.001) C、0.050(精确到0.001) D、0.0502(精确到0.0001)6. 下列说法正确的是( )A、绝对值最小的实数是0 B、带根号的都是无理数 C、无限小数是无理数 D、 是分数7. 下列说法中错误的是( )A、一个数同0相乘,仍得0 B、一个数同1相乘,仍得原数 C、一个数同-1相乘,得原数的相反数 D、互为相反数的两个数的积是18. 在3.14, , , , , ,0.818118111811118……(相邻两个8 之间依次多一个1),这7个实数中无理数的个数为( )A、3 B、4 C、5 D、69. 有一个两位数,十位数字是 ,个位数字是 ,若把它们的位置交换,得到新的两位数是( )
4. 今年余姚市上半年接待国内外游客650多万人次,实现旅游总收入61亿元,其中,61亿用科学记数法表示是( )A、 B、 C、 D、5. 按要求对0.05019分别取近似值,下面结果错误的是( )A、0.1(精确到0.1) B、0.05(精确到0.001) C、0.050(精确到0.001) D、0.0502(精确到0.0001)6. 下列说法正确的是( )A、绝对值最小的实数是0 B、带根号的都是无理数 C、无限小数是无理数 D、 是分数7. 下列说法中错误的是( )A、一个数同0相乘,仍得0 B、一个数同1相乘,仍得原数 C、一个数同-1相乘,得原数的相反数 D、互为相反数的两个数的积是18. 在3.14, , , , , ,0.818118111811118……(相邻两个8 之间依次多一个1),这7个实数中无理数的个数为( )A、3 B、4 C、5 D、69. 有一个两位数,十位数字是 ,个位数字是 ,若把它们的位置交换,得到新的两位数是( )
A、 B、 C、 D、10. 小明同学设计了一个计算程序,如图,如果输入的数是2,那么输出的结果是( ) A、-2 B、2 C、-6 D、611. 将 , , 从小到大排列正确的是( )
A、-2 B、2 C、-6 D、611. 将 , , 从小到大排列正确的是( )
A、 B、 C、 D、12. 下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )A、495 B、497 C、501 D、503二、填空题
-
13. -7的绝对值是.14. 的平方根等于.15. 数轴上点A对应的数为﹣2,与点A相距5个单位长度的点所对应的数为 .16. 化简:|π-4|+|3-π|= .17. 用“★”定义新运算:对于任意有理数 、 都有 ★ ,例如7★4= =17,那么 ★( ★2)=.18. 已知 的小数部分为 , 的小数部分为 ,则 =.
三、解答题
-
19. 计算
(1)、(2)、20. 计算
(1)、(2)、
21. 画数轴,并将下列各数及其相反数表示在数轴上,再把所有的数按照从小到大的顺序用“<”连接.,-3,5, ,
22. 在一次数学测验中,七年级(4)班的平均分为86分,如果把高于平均分的部分记作正数,不足平均分的部分记作负数
(1)、李洋得了90分,应记作多少?
(2)、刘红的成绩记作-5分,她实际得分是多少?
(3)、李洋和刘红相差多少分?
23. 出租车司机小李某天下午营运全是在东西走向的大道上行驶,如果规定向东行驶为正,向西行驶为负,这天下午行车里程如下(单位:千米):+10,-3,+16,-11,+12,-10,+5,-15,
+18,-16
(1)、当最后一名乘客被送到目的地时,与出车地点的距离为多少千米?(2)、若每千米的营业额为7元,则这天下午营业额为多少?
24. 如图1,这是由8个同样大小的立方体组成的魔方,体积为64. (1)、求出这个魔方的棱长.(2)、图中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.(3)、把正方形ABCD放到数轴上,如图2,使得A与﹣1重合,那么D在数轴上表示的数为.
(1)、求出这个魔方的棱长.(2)、图中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.(3)、把正方形ABCD放到数轴上,如图2,使得A与﹣1重合,那么D在数轴上表示的数为. 25. 阅读下面的文字,完成后面的问题:
25. 阅读下面的文字,完成后面的问题:我们知道: , ,
那么
(1)、 ; ;(2)、用含有 的等式表示你发现的规律;(3)、如果 ,求 的值.26. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础。小白在草稿纸上画了一条数轴进行操作探究: (1)、操作一:
(1)、操作一:折叠纸面,若使1表示的点与﹣1表示的点重合,则﹣2表示的点与表示的点重合;
(2)、操作二:折叠纸面,若使1表示的点与﹣3表示的点重合,回答以下问题:
①3表示的点与表示的点重合;
②若数轴上A、B两点之间距离为7(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是;
(3)、操作三:在数轴上剪下9个单位长度(从﹣1到8)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(例如下图). 若这三条线段的长度之比为1:1:2,则折痕处对应的点所表示的数可能是.