云南省昆明市昆十中2017-2018学年上七年级上学期数学期中考试试卷

试卷更新日期：2018-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. $- 2017$ 的相反数是（）

A、 $- 2017$ B、 $2017$ C、 $- \frac{1}{2017}$ D、 $\frac{1}{2017}$

查看试题解析
2. 多项式 $π a^{5} - 3 a^{3} b^{2} + 2^{8}$ 是（）

A、六次三项式 B、八次三项式 C、五次二项式 D、五次三项式

查看试题解析
3. 下列运算正确的是（）

A、5xy-4xy=1 B、3x²+2x³=5x⁵ C、x²-x=x D、3x²+2x²=5x²

查看试题解析
4. 下列说法正确的有（）
①所有的有理数都能用数轴上的点表示；②符号不同的两个数互为相反数；③有理数分为正数和负数；④两数相减，差一定小于被减数；⑤两数相加，和一定大于任何一个加数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 在下列式子-2x+2，-1，x，x²-3x+2，π， $\frac{5}{x}$ ， $\frac{x + y}{7}$ 中，整式有（）

A、4个 B、5个 C、6个 D、7个

查看试题解析
6. 近似数5.0×10²精确到（）

A、十分位 B、个位 C、十位 D、百位

查看试题解析
7. 下列各数：（-3）² ， 0， $- {(- \frac{1}{2})}^{2}$ ， $\frac{22}{7}$ ，（-1）²⁰⁰⁹ ， -2² ， -（-8）， $- |- \frac{3}{4} |$ 中，负数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 表示a，b两数的点在数轴上位置如图所示，则下列判断错误的是（）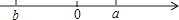

A、a+b＜0 B、a﹣b＞0 C、a×b＞0 D、a＜|b|

查看试题解析
9. 数轴上，表示-5的点为A，则与A的距离是2的点B所表示的数是（）

A、-3 B、-7 C、±3 D、-7或-3

查看试题解析

二、填空题

10. 若李明同学家里去年收入6万元，记作+6万元，则去年支出4万元，记作万元．

查看试题解析
11. -2.5的倒数是。

查看试题解析
12. 比较大小： $- \frac{5}{6}$ $- \frac{6}{7}$ （用不等号填空）。

查看试题解析
13. 单项式 $- \frac{2 π a^{2} b}{3}$ 的系数是。

查看试题解析
14. 中国的领水面积约为370 000 km² ，将数370 000用科学记数法表示为：。

查看试题解析
15. 某种圆形零件的尺寸要求是 $ϕ ： 20 \pm 0.02$ mm（φ表示其直径，单位是毫米），经检查，某个零件的直径是19.9mm，该零件（填“合格”或“不合格”）

查看试题解析
16. 若 $- \frac{1}{2} x^{m + 3} y$ 与 $2 x^{4} y^{n + 3}$ 是同类项，则（m+n）²⁰¹⁷= ．

查看试题解析
17. 若|a|＝3，|b|＝5，且ab＜0，则a＋b＝．

查看试题解析
18. 已知多项式x+2y-1的值是3，则多项式3-x-2y的值是。

查看试题解析
19. 已知x，y为有理数，现规定一种新运算△，满足x△y=xy+1，则（1△4）△（-2）=。

查看试题解析

三、解答题

20. 把下列各数分别填在表示它所在的集合里：
$\frac{1}{2} ， 5.2 ， 0 ， \frac{2}{π} ， \frac{22}{7} ， - 2^{2} ， - \frac{5}{2} ， 2005 ， - 0.03$

(1)、整数集合：{                                ··· }

(2)、分数集合集合：{                               ··· }

(3)、非负的整数集合集合：{                                 ···}

(4)、非负有理数集合集合：{                                 ···}

查看试题解析
21. 计算：

(1)、 $7 \frac{3}{4} + (- 5 \frac{4}{11}) - (- 3 \frac{1}{4}) + 6 \frac{7}{11}$ ；

(2)、 $- 1^{4} - (- 5 \frac{1}{2}) \times \frac{4}{11} + {(- 2)}^{3} \div [- 3^{2} + 1]$ ；

(3)、 ${(- \frac{1}{4})}^{2} \div (- \frac{1}{2})$

查看试题解析
22. 计算：

(1)、 $x^{2} + 5 y - (4 x^{2} - 3 y - 1)$

(2)、 $3 (4 x^{2} - 3 x + 2) - 2 (- 4 x^{2} + 1 + x)$

查看试题解析
23. 先化简，再求值：
求 $2 x^{2} - [3 (- \frac{1}{3} x^{2} + \frac{2}{3} x y) - 2 y^{2}] - 2 (x^{2} - x y + 2 y^{2})$ 的值，其中 $x = \frac{1}{2}$ ，y=-1.

查看试题解析
24. 小明早晨跑步，他从自己家出发，向东跑了2km到达小彬家，继续向东跑了1.5km到达小红家，然后又向西跑了4.5km到达学校，最后又向东，跑回到自己家．

(1)、以小明家为原点，以向东为正方向，用1个单位长度表示1km，在图中的数轴上，分别用点A表示出小彬家，用点B表示出小红家，用点C表示出学校的位置；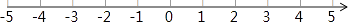

(2)、求小彬家与学校之间的距离；

(3)、如果小明跑步的速度是250m/min，那么小明跑步一共用了多长时间？

查看试题解析
25. 股民周思源上周五在股市以收盘价（收市时的价格）买进某公司股票1000股，每股25元，周六、周日股市不交易，在接下来的一周交易日内，周思源记下该股票每日收盘价格相比前一天的涨跌情况：（单位：元）
星期
一
二
三
四
五
每股涨跌（元）
+2
-1.4
+0.9
-1.8
+0.5
根据上表回答问题：

(1)、星期二收盘时，该股票每股多少元？

(2)、这一周内该股票收盘时的最高价，最低价分别是多少？

(3)、已知买入股票与卖出股票均需支付成交总金额的5‰（千分之五）的交易费，若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？

查看试题解析
26. 已知某个长方形的周长为6m，长为2m+n.

(1)、用含m，n的整式表示该长方形的宽；

(2)、若m，n满足（m-6）²+|n-4|=0，求该长方形的面积.

查看试题解析
27. 观察下面的三行数：
2，4，6，8，10，12，···； ①
3，5，7，9，11，13，···； ②
6，12，18，24，30，36，···； ③

(1)、第①行数按什么规律排列？

(2)、第②，③行数与第①行数分别有什么关系？

(3)、取每行数的第n个数，用含n的式子表示出每行数的第n个数（共三个），计算这三个式子的和。当n=100时，求此和的值。

查看试题解析

星期	一	二	三	四	五
每股涨跌（元）	+2	-1.4	+0.9	-1.8	+0.5