沪科版八年级数学上册第一次月考试卷
试卷更新日期:2018-11-21 类型:月考试卷
一、选择题
-
1. 如图所示,网格中画有一张脸,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
 A、(1,0) B、(-1,0) C、(-1,1) D、(1,-1)2. 在函数 中,自变量x的取值范围是( )
A、(1,0) B、(-1,0) C、(-1,1) D、(1,-1)2. 在函数 中,自变量x的取值范围是( )
A、x≥5 B、x≤5 C、x>5 D、x<53. 如图,线段AB经过平移得到线段A1B1 , 其中点A,B的对应点分别为点A1 , B1 , 这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P′的坐标为( )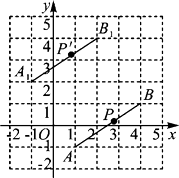 A、(a-2,b+3) B、(a-2,b-3) C、(a+2,b+3) D、(a+2,b-3)4. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量Q(升)与行驶时间(t小时)之间的函数关系图象是( )A、
A、(a-2,b+3) B、(a-2,b-3) C、(a+2,b+3) D、(a+2,b-3)4. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量Q(升)与行驶时间(t小时)之间的函数关系图象是( )A、 B、
B、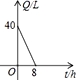 C、
C、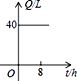 D、
D、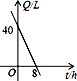 5. 已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为( )A、(4,﹣2) B、(﹣4,2) C、(﹣2,4) D、(2,﹣4)6. 在球的体积公式V= πr3中,下列说法正确的是( )A、V、π、r是变量, 是常量 B、V、r是变量, 是常量 C、V、r是变量, π是常量 D、以上都不对7. 数轴上的点M对应的数是-2,那么将点M向右移动4个单位长度,此时点M表示的数是( )A、-6 B、2 C、-6或2 D、都不正确8. 排列做操队形时,甲、乙、丙位置如图所示,甲对乙说,如果我的位置用(0,0)来表示,你的位置用(2,1)表示,那么丙的位置是( )
5. 已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为( )A、(4,﹣2) B、(﹣4,2) C、(﹣2,4) D、(2,﹣4)6. 在球的体积公式V= πr3中,下列说法正确的是( )A、V、π、r是变量, 是常量 B、V、r是变量, 是常量 C、V、r是变量, π是常量 D、以上都不对7. 数轴上的点M对应的数是-2,那么将点M向右移动4个单位长度,此时点M表示的数是( )A、-6 B、2 C、-6或2 D、都不正确8. 排列做操队形时,甲、乙、丙位置如图所示,甲对乙说,如果我的位置用(0,0)来表示,你的位置用(2,1)表示,那么丙的位置是( )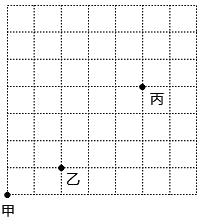 A、(5,4) B、(4,5) C、(3,4) D、(4、3)9. 已知点M(3,﹣2)与点M′(x,y)在同一条平行于x轴的直线上,且M′到y轴的距离等于4,那么点M′的坐标是( )A、(4,2)或(﹣4,2) B、(4,﹣2)或(﹣4,﹣2) C、(4,﹣2)或(﹣5,﹣2) D、(4,﹣2)或(﹣1,﹣2)10. 点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度得到点A′,则点A′的坐标是( )A、(3,3) B、(-1,3) C、(-1,-1) D、(3,1)11. 如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
A、(5,4) B、(4,5) C、(3,4) D、(4、3)9. 已知点M(3,﹣2)与点M′(x,y)在同一条平行于x轴的直线上,且M′到y轴的距离等于4,那么点M′的坐标是( )A、(4,2)或(﹣4,2) B、(4,﹣2)或(﹣4,﹣2) C、(4,﹣2)或(﹣5,﹣2) D、(4,﹣2)或(﹣1,﹣2)10. 点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度得到点A′,则点A′的坐标是( )A、(3,3) B、(-1,3) C、(-1,-1) D、(3,1)11. 如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )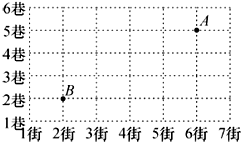 A、(2,2)→(2,5)→(5,6) B、(2,2)→(2,5)→(6,5) C、(2,2)→(6,2)→(6,5) D、(2,2)→(2,3)→(6,3)→(6,5)12. 教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:
A、(2,2)→(2,5)→(5,6) B、(2,2)→(2,5)→(6,5) C、(2,2)→(6,2)→(6,5) D、(2,2)→(2,3)→(6,3)→(6,5)12. 教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:①乙组教师获胜②乙组教师往返用时相差2秒③甲组教师去时速度为0.5米/秒④返回时甲组教师与乙组教师的速度比是2:3
其中合理的是( )
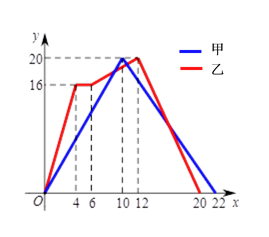 A、①② B、①③ C、②④ D、①④
A、①② B、①③ C、②④ D、①④二、填空题
-
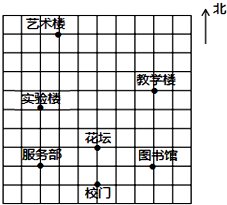
13. 如果电影票上的“3排4号”记作(3,4),那么(4,3)表示排号。14. 若函数 有意义,则自变量x的取值范围是。15. 已知点A(-1,1),若将它先向右平移2个单位,再向上平移3个单位得到点B,则点B的坐标是;16. 已知平行四边形的三个顶点坐标分别为(-1,0)、(0,2)(2,0),则第四个顶点的坐标为.17. 如图是某校的平面示意图,如果分别用(3,﹣1)、(﹣3,2)表示图中图书馆和实验楼的位置,那么校门的位置可表示为 .
 18. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),按这样的运动规律,经过第2017次运动后,动点P的坐标是 , 经过第2018次运动后,动点P的坐标是 .
18. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),按这样的运动规律,经过第2017次运动后,动点P的坐标是 , 经过第2018次运动后,动点P的坐标是 .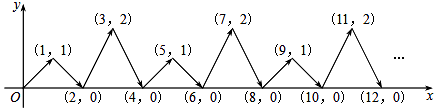
三、解答题
-
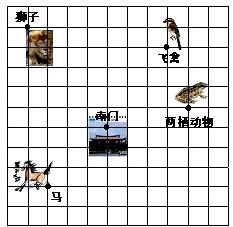
19. 这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
 20. 在平面直角坐标系中,已知A(﹣1,1),B(3,4),C(3,8).(1)、建立平面直角坐标系,描出A、B、C三点,求出三角形ABC的面积;(2)、求出三角形ABO(若O是你所建立的坐标系的原点)的面积.21. 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
20. 在平面直角坐标系中,已知A(﹣1,1),B(3,4),C(3,8).(1)、建立平面直角坐标系,描出A、B、C三点,求出三角形ABC的面积;(2)、求出三角形ABO(若O是你所建立的坐标系的原点)的面积.21. 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题: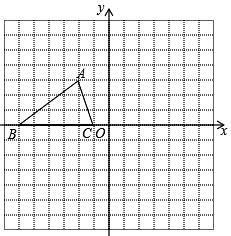 (1)、A点的坐标为; B点的坐标为;C点的坐标为.(2)、将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.(3)、△A' B' C'与△ABC的位置关系是.22. 如图,三角形ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)、A点的坐标为; B点的坐标为;C点的坐标为.(2)、将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.(3)、△A' B' C'与△ABC的位置关系是.22. 如图,三角形ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).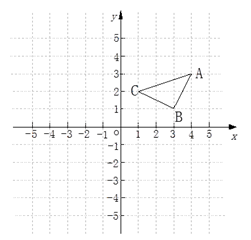 (1)、把三角形ABC向左平移6个单位长度,则点A的对应点A1的坐标是( , ),点B的对应点B1的坐标是( , ),点C的对应点C1的坐标是( , ),在图中画出平移后的三角形A1B1C1;(2)、把三角形ABC向下平移5个单位长度,则点A的对应点A2的坐标是( , -2),点B的对应点B2的坐标是( , ),点C的对应点C2的坐标是( , ),在图中画出平移后的三角形A2B2C2.23. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)、把三角形ABC向左平移6个单位长度,则点A的对应点A1的坐标是( , ),点B的对应点B1的坐标是( , ),点C的对应点C1的坐标是( , ),在图中画出平移后的三角形A1B1C1;(2)、把三角形ABC向下平移5个单位长度,则点A的对应点A2的坐标是( , -2),点B的对应点B2的坐标是( , ),点C的对应点C2的坐标是( , ),在图中画出平移后的三角形A2B2C2.23. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).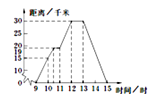
 (1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、10时和13时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、11时到12时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?24. 如图所示的图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:
(1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、10时和13时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、11时到12时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?24. 如图所示的图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题: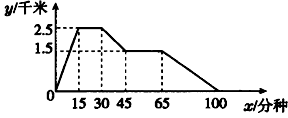 (1)、体育场离小明家多远?小明从家到体育场用了多少时间?(2)、体育场离文具店多远?(3)、小明在文具店逗留了多少时间?(4)、小明从文具店回家的平均速度是多少?25. 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)、体育场离小明家多远?小明从家到体育场用了多少时间?(2)、体育场离文具店多远?(3)、小明在文具店逗留了多少时间?(4)、小明从文具店回家的平均速度是多少?25. 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: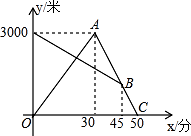 (1)、求张强返回时的速度;(2)、妈妈比按原速返回提前多少分钟到家?(3)、请直接写出张强与妈妈何时相距1200米?26. 某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)、分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的关系式;(2)、对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜.
(1)、求张强返回时的速度;(2)、妈妈比按原速返回提前多少分钟到家?(3)、请直接写出张强与妈妈何时相距1200米?26. 某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).(1)、分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的关系式;(2)、对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜.