浙江省瑞安市五校2017届九年级上学期数学期中联考试卷
试卷更新日期:2018-11-21 类型:期中考试
一、单选题
-
1. 抛物线 与y轴的交点坐标是( )A、(0,1) B、(0,-1) C、(1,0) D、(-1,0)2. 如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为( )
 A、80° B、70° C、60° D、40°3. 将抛物线 向右平移2个单位所得抛物线的函数表达式为( )A、 B、 C、 D、4.
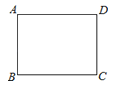
A、80° B、70° C、60° D、40°3. 将抛物线 向右平移2个单位所得抛物线的函数表达式为( )A、 B、 C、 D、4.如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是( )
 A、点A B、点B C、点C D、点D5. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度为( )
A、点A B、点B C、点C D、点D5. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度为( ) A、1 cm B、2 cm C、3cm D、4cm6. 如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
A、1 cm B、2 cm C、3cm D、4cm6. 如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( ) A、 B、 C、 D、7. 如图,已知抛物线 的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值 时,自变量x的取值范围是( )
A、 B、 C、 D、7. 如图,已知抛物线 的顶点为(2,-1),抛物线与y轴的交点为(0,3),当函数值 时,自变量x的取值范围是( ) A、 B、 C、 D、8. 如图,AB为半圆O的直径,C、D是半圆上的两点,且D是
A、 B、 C、 D、8. 如图,AB为半圆O的直径,C、D是半圆上的两点,且D是 的中点,连接AC,若∠B=70°,则∠DAB的度数为( )
的中点,连接AC,若∠B=70°,则∠DAB的度数为( ) A、54° B、55° C、56° D、57°9. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
A、54° B、55° C、56° D、57°9. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )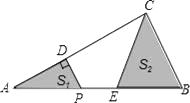 A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小
A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小二、填空题
-
10. 已知抛物线 的对称轴是直线 ,则 的值为 .11. 一个不透明的袋子中装有3个红球和若干个白球,它们除颜色外其余都相同.现随机从袋中摸出一个球,若颜色是白色的概率为 ,则袋中白球的个数是 .
12. 如图,已知AB和CD是⊙O的两条直径,CE∥AB,若 弧 的度数为40°,则 的度数为 . 13. 如图,经过原点的⊙P与x轴,y轴分别交于A(3,0),B(0,4)两点,点C是 上一点,且BC=2,则AC= .
13. 如图,经过原点的⊙P与x轴,y轴分别交于A(3,0),B(0,4)两点,点C是 上一点,且BC=2,则AC= .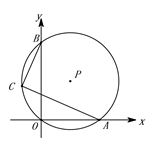 14. 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为m2 .
14. 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为m2 .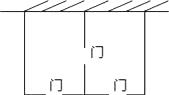 15. 如图,点A是抛物线 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为 .
15. 如图,点A是抛物线 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为 .
三、解答题
-
16. 已知△ABC顶点都在4×4的正方形网格格点上,如图所示.
 (1)、请画出△ABC的外接圆,并标明圆心O的位置;(2)、这个圆中弦BC所对的圆周角的度数是 .
(1)、请画出△ABC的外接圆,并标明圆心O的位置;(2)、这个圆中弦BC所对的圆周角的度数是 .
17. 如图,均匀的正四面体的各面依次有1,2,3,4四个数字,小明做了60次投掷试验,结果统计如下:朝下数字
1
2
3
4
出现的次数
16
20
14
10
 (1)、计算上述试验中“4朝下”的频率;(2)、“根据试验结果,投掷一次正四面体,出现数字2朝下的概率是 ”,这种说法正确吗?为什么?18. 已知:如图,AB,AC是⊙O的两条弦,AO平分∠BAC.
(1)、计算上述试验中“4朝下”的频率;(2)、“根据试验结果,投掷一次正四面体,出现数字2朝下的概率是 ”,这种说法正确吗?为什么?18. 已知:如图,AB,AC是⊙O的两条弦,AO平分∠BAC.求证: .
 19. 如图,抛物线 与 轴相交于点A、B,且过点C(4,3).
19. 如图,抛物线 与 轴相交于点A、B,且过点C(4,3). (1)、求 的值和该抛物线顶点P的坐标;(2)、将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.
(1)、求 的值和该抛物线顶点P的坐标;(2)、将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.
20. 为了在校体育节的排球比赛上取得好成绩,甲、乙、丙、丁四人一起训练传接球.传接球规则如下:接球者把球随机传给另外三人中的一人.现由甲开始传球,请回答下列问题(假设每次传球都能接到球):
(1)、写出第一次接球者是乙的概率;
(2)、用列表或画树状图的方法求第二次接球者是甲的概率.
21. 如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m. (1)、若AB为1m,直接写出此时窗户的透光面积m2;(2)、设AB=x,求窗户透光面积S关于x的函数表达式,并求出S的最大值.22. 如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
(1)、若AB为1m,直接写出此时窗户的透光面积m2;(2)、设AB=x,求窗户透光面积S关于x的函数表达式,并求出S的最大值.22. 如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD, (1)、求证:点E是 的中点;
(1)、求证:点E是 的中点;
(2)、当BC=12,且AD:CD=1:2时,求⊙O的半径.
23. 如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0). (1)、求抛物线的函数表达式;(2)、当0<x<3时,求线段CD的最大值;
(1)、求抛物线的函数表达式;(2)、当0<x<3时,求线段CD的最大值;
(3)、在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;(4)、过点B,C,P的外接圆恰好经过点A时,x的值为 . (直接写出答案)个