广西柳州市柳江区2018届九年级上学期数学期中考试试卷
试卷更新日期：2018-11-21 类型：期中考试
一、单选题
-
1. 一元二次方程 的解是（ ）
A、x=0 B、 =2 C、 ， D、x=22. 下列图案中，不是中心对称图形的是（ ）
A、
B、
C、
D、
3. 抛物线y=﹣x2开口方向是（ ）
A、向上 B、向下 C、向左 D、向右4. 用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（ ）A、（x+1）2=6 B、（x+2）2=9 C、（x﹣1）2=6 D、（x﹣2）2=95. 二次函数y=﹣2（x﹣1）2+3的图象的顶点坐标是（ ）A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（﹣1，﹣3）6. 如图，四边形ABCD是正方形，△ADE绕着点A旋转90°后到达△ABF的位置，连接EF，则△AEF的形状是（ ）
A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形7. 一元二次方程x2+2x+2=0的根的情况是（ ）
A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、无实数根8. 若将抛物线y=x2向右平移2个单位，再向上平移3个单位，则所得抛物线的表达式为（ ）
A、y=（x+2）2+3 B、y=（x﹣2）2+3 C、y=（x+2）2﹣3 D、y=（x﹣2）2﹣39. 某校成立“情暖校园”爱心基金会，去年上半年发给每个经济困难的学生600元，今年上半年发给了800元，设每半年发给的资金金额的平均增长率为x，则下面列出的方程中正确的是（ ）A、800（1﹣x）2=600 B、600（1﹣x）2=800 C、800（1+x）2=600 D、600（1+x）2=80010. 设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+1上的三点，则y1 ， y2 ， y3的大小关系为（ ）A、y1＞y2＞y3 B、y1＞y3＞y2 C、y3＞y2＞y1 D、y3＞y1＞y211. 如图，△ABC中，将△ABC绕点A顺时针旋转40°后，得到△AB′C′，且C′在边BC上，则∠AC′C的度数为（ ）
A、50° B、60° C、70° D、80°12. 二次函数y=ax2+bx+c的图象如图所示，则一次函数y=bx+a的图象不经过（ ）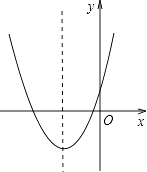
A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
13. 点（﹣2，1）关于原点对称的点的坐标为 ．14. 二次函数y＝2(x－3)2－4的最小值为 ．
15. 若x=2是一元二次方程x2+x﹣a=0的解，则a的值为 ．16. 16．若函数 是二次函数，则m的值为 ．
17. 已知方程5x2+kx﹣10=0的一个根是﹣5，则它的另一个根是 ．
18. 在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4．则下列四个结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△AED的周长是9．其中正确的结论是（把你认为正确结论的序号都填上．）
三、解答题
-
19. 解下列方程：
(1)、x2=2x，(2)、x2﹣6x+5=0．20. 如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC．
①作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1 ， （只画出图形）．
②作出△ABC关于原点O成中心对称的△A2B2C2 ， （只画出图形），写出B2和C2的坐标．
21. 如图，在△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O逆时针方向旋转90°得到△OA1B1 ．
(1)、线段A1B1的长是；∠AOB1的度数是 ．
(2)、连接AA1 ， 求证：四边形OAA1B1是平行四边形．22. 已知函数图象如图所示，根据图象可得：
(1)、抛物线顶点坐标；(2)、对称轴为；
(3)、当x=时，y有最大值是；
(4)、当时，y随着x得增大而增大。
(5)、当时，y＞0.
23. 如图，△ABC中，AB=AC=2，∠BAC=45°，△AEF是由△ABC绕点A按逆时针方向旋转得到的，连接BE、CF相交于点D，求证：BE=CF．
24. 已知抛物线的解析式为y=x2﹣（2m﹣1）x+m2﹣m
(1)、求证：此抛物线与x轴必有两个不同的交点；
(2)、若此抛物线与直线y=x﹣3m+4的一个交点在y轴上，求m的值．
25. 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件．
(1)、若商场平均每天要盈利1600元，每件衬衫应降价多少元？(2)、若该商场要每天盈利最大，每件衬衫应降价多少元？盈利最大是多少元？
26. 已知：二次函数y=x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．
(1)、求抛物线的解析式；(2)、抛物线的对称轴上有一动点P，求出PA+PD的最小值；
(3)、若抛物线上有一动点P，使三角形ABP的面积为6，求P点坐标．