广西来宾市忻城县2018届九年级上学期数学期中考试试卷

试卷更新日期：2018-11-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数：① $y = \frac{x}{2}$ ；② $y = \frac{2}{x}$ ；③ $y = - \frac{1}{2 x}$ ；④ $y = 2 x^{- 1}$ 中，是反比例函数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 已知反比例函数的图象经过点P(-2，4)，则此反比例函数的解析式是（）

A、 $y = \frac{8}{x}$ B、 $y = - \frac{8}{x}$ C、 $y = \frac{x}{8}$ D、 $y = - \frac{x}{8}$

查看试题解析
3. 一元二次方程 $3 x - 2 = x (2 x - l)$ 的一般形式是（）

A、 $2 x^{2} - 3 x - 2 = 0$ B、 $2 x^{2} + 3 x - 2 = 0$ C、 $2 x^{2} - 4 x - 2 = O$ D、 $2 x^{2} - 4 x + 2 = 0$

查看试题解析
4. 若关于x的一元二次方程 $x^{2} + 3 x + a = 0$ 的一个根是-2，则另一个根为（）

A、5 B、-1 C、2 D、-5

查看试题解析
5. 一元二次方程2(2-x)(x+3)=9的二次项、一次项、常数项分别是（）

A、2 $x^{2}$ 、2x、-3 B、2 $x^{2}$ 、2x、21 C、2、2、-3 D、2、2、21

查看试题解析
6. 方程：2 ${(x + 3)}^{2}$ =8的解是（）

A、 $x_{1} = 2$ ， $x_{2} = - 2$ B、 $x_{1} = 5$ ， $x_{2} = 1$ C、 $x_{1} = - 1$ ， $x_{2} = - 5$ D、 $x_{1} = 1$ ， $x_{2} = - 7$

查看试题解析
7. 一元二次方程：2 $x^{2}$ + 4x +1=0的根的情况是（）

A、有两个不相等的实数根 B、有一个实数根 C、有两个相等的实数根 D、没有实数根

查看试题解析
8. 已知一元二次方程的两个根是2和-3，则这个一元二次方程是（）

A、 $x^{2} + x + 6 = 0$ B、 $x^{2} + x - 6 = 0$ C、 $x^{2} - x + 6 = 0$ D、 $x^{2} - x - 6 = 0$

查看试题解析
9. 已知一元二次方程 $x^{2}$ -5x-6=0的两根分别为 $x_{1}$ 和 $x_{2}$ ，则 $x_{1} + x_{2}$ 的值是（）

A、5 B、-5 C、6 D、-6

查看试题解析
10. 已知： $\frac{a}{b} = \frac{2}{3}$ ，下列式子中错误的是（）

A、 $\frac{b}{a} = \frac{3}{2}$ B、 $\frac{a + b}{b} = \frac{5}{3}$ C、 $\frac{a - b}{b} = - \frac{1}{3}$ D、 $\frac{a - 1}{b - 1} = \frac{1}{2}$

查看试题解析
11. 如图，△ABC中，DE∥AB，则下列式子中错误的是（）

A、 $\frac{CD}{AD} = \frac{CE}{BE}$ B、 $\frac{CD}{AC} = \frac{CE}{BC}$ C、 $\frac{DE}{AB} = \frac{CD}{AD}$ D、 $\frac{DE}{AB} = \frac{CE}{BC}$

查看试题解析
12. 如图，□ABCD中，E是AD延长线上一点，BE交AC于点F ，交DC于点G ，则下列结论中错误的是（　　）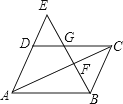

A、△ABE∽△DGE B、△CGB∽△DGE C、△BCF∽△EAF D、△ACD∽△GCF

查看试题解析

二、填空题

13. 反比例函数y= $- \frac{3}{x}$ 图象经过点A( $x_{1}$ ， $y_{1}$ )和B( $x_{2}$ ， $y_{2}$ )，且 $x_{1} > x_{2} > 0$ .则 $y_{1}$ 与 $y_{2}$ 的大小关系是．

查看试题解析
14. 如图，△ABC中，D是边AB上一点，要使△ABC∽△ACD，添加一个条件，你所添加的条件是．

查看试题解析
15. 已知8：x =6：9，则x的值等于。

查看试题解析
16. 三角形两边的长是3和4，第三边的长是方程x²﹣12x+35=0的根，则该三角形的周长为．

查看试题解析
17. 设 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - 3 x - 7 = 0$ 的两根，则 $x_{1}^{2} + x_{2}^{2} + 4 x_{1} x_{2}$ 的值为．

查看试题解析
18. 如图，点p在反比例y= $\frac{2}{x}$ 的图象上，且OP=4，过点P作PA $⊥$ x轴于点A，则△OPA的周长等于．

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $2 {(x - 2)}^{2}$ $= 3 (2 - x)$

(2)、 $5 x^{2} - 4 x = 12$

查看试题解析
20. 已知反比例函数的图象经过P（-2·3）．

(1)、求此反比例函数的解析式；

(2)、点A(2．-3)、B(3，2)是否在这个函数的图象上？

(3)、这个函数的图象位于哪些象限？函数值y随自变量x的减小如何变化？

查看试题解析
21. 关于x的方程 ${kx}^{2} + (k + 2) x + \frac{k}{4} = 0$ 有两个不相等的实数根．

(1)、求k的取值范围。

(2)、是否存在实数k，使方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．

查看试题解析
22. 如图，在Rt△ABC中，∠ACB=90 $°$ ，CD $⊥$ AB于D．

(1)、写出图中相似的三角形；

(2)、求证： ${CD}^{2}$ = AD·BD ．

查看试题解析
23. 某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光明且温度为18 $℃$ 的条件下生长最快的新品种．如图，是某天恒温系统从开启到关闭及关闭后，大棚内温度y( $℃$ )随时间x(小时)变化的函数图象，其中BC段足双曲线 $y = \frac{k}{x}$ 的一部分，请根据图中信息解答下列问题：

(1)、恒温系统这天保持大棚内温度18 $℃$ 的时间有多少小时？

(2)、求k值；

(3)、当x=15时，大棚内的温度约为多少度？

查看试题解析
24. 如图，在△ABC中，D、E分别是边AC、BC的中点，F是BC延长线上一点，∠F=∠B．

(1)、若AB=1O，求FD的长；

(2)、若AC=BC．求证：△CDE∽△DFE .

查看试题解析
25. 如图，四边形ABCD中AC平分∠BAD，∠ADC=∠ACB= $90 °$ ，E为AB的中点，AC与DE交于点F．

(1)、求证： $A C^{2}$ =AB·AD；

(2)、求证：CE//AD；

(3)、若AD=6， AB=8．求 $\frac{A C}{A F}$ 的值．

查看试题解析
26. 某特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：

(1)、每千克核桃应降价多少元？

(2)、在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？

查看试题解析