广西桂林一中2018届九年级上学期数学期中考试试卷
试卷更新日期:2018-11-21 类型:期中考试
一、单选题
-
1. 下列函数关系式中属于反比例函数的是( )A、y=3x B、y=﹣ C、y=x2+3 D、x+y=52. 关于x的方程3x2﹣2x﹣5=0的二次项系数和一次项系数分别是( )
A、3,﹣2 B、3,2 C、3,5 D、5,23. 下列各点中,在函数y=﹣ 图象上的是( )
A、(-2,-4) B、(2,3) C、(﹣1,6) D、(﹣ ,3)4. 一元二次方程2x2+x﹣3=0的根的情况是( )
A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定5. 已知函数 的图象过点(1,-2),则该函数的图象必在( )
A、第二、三象限 B、第二、四象限 C、第一、三象限 D、第三、四象限6. 下列四条线段中,不能成比例的是( )
A、a=3,b=6,c=2,d=4 B、a=1,b= ,c= ,d=4 C、a=4,b=5,c=8,d=10 D、a=2,b=3,c=4,d=57. 反比例函数y= 图象上有三个点(﹣2,y1),(﹣1,y2),(1,y3),则y1 , y2 , y3的大小关系是( )
A、y1<y2<y3 B、y3<y1<y2 C、y2<y1<y3 D、y3<y2<y18. 用配方法解方程x2﹣2x﹣4=0时,配方后所得的方程为( )
A、(x﹣1)2=0 B、(x﹣1)2=5 C、(x+1)2=0 D、(x+1)2=59. 某商品原价200元,连续两次降价a%后售价为108元,下列所列方程正确的是( )
A、200(1+a%)2=108 B、200(1﹣a2%)=108 C、200(1﹣2a%)=108 D、200(1﹣a%)2=10810. 如图, 在同一坐标系中(水平方向是x轴),函数 和 的图象大致是( )
A、 B、
B、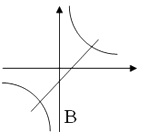 C、
C、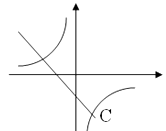 D、
D、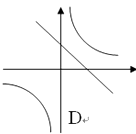 11. 如图,函数y1 =x-l和函数y2= 的图像相交于点M(2,m),N(-1,n),若y1>y2 , 则x的取值范围是( )
11. 如图,函数y1 =x-l和函数y2= 的图像相交于点M(2,m),N(-1,n),若y1>y2 , 则x的取值范围是( )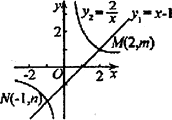 A、x< -1或0<x<2 B、x<-1或x>2 C、 -1<x<0或0<x<2 D、-1<x<0或x>2
A、x< -1或0<x<2 B、x<-1或x>2 C、 -1<x<0或0<x<2 D、-1<x<0或x>2二、填空题
-
12. 若 2:3=x:9,则x= .
13. 把一元二次方程3x(x﹣2)=4化为一般形式是 .
14. 点P(1,3)在反比例函数y= (k≠﹣1)图象上,则k= .
15. 若关于x的方程x2+3x+a=0有一个根为﹣1,则另一个根为 .16. 如图,已知点C为反比例函数图象上的一点,过点C向坐标轴引垂线,垂足为A、B,四边形AOBC的面积为6,则反比例函数的解析式为 .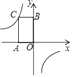 17. 观察下列图形规律:当n=时,图形“●”的个数和“△”的个数相等.
17. 观察下列图形规律:当n=时,图形“●”的个数和“△”的个数相等.
三、解答题
-
18. 解下列方程
(1)、x2﹣2x=0(2)、x2+3x=4.19. 已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a﹣2b+3c的值.
20. 已知如图,直线AD∥BE∥CF ,DE=6,求EF的长.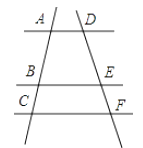 21. 已知关于x的一元二次方程x2﹣2x﹣a=0.
21. 已知关于x的一元二次方程x2﹣2x﹣a=0.
(1)、如果此方程有两个不相等的实数根,求a的取值范围;(2)、如果此方程的两个实数根为x1 , x2 , 且满足 ,求a的值.22. 某小区2013年屋顶绿化面积为2000平方米,计划2015年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是多少?23. 已知函数y= 为反比例函数.
(1)、求k的值;(2)、它的图象在第象限内,在各象限内,y随x增大而;(填变化情况)
(3)、求出﹣2≤x≤﹣ 时,y的取值范围.
24. 将进货单价为40元的商品按50元售出时,能卖出500个,已知这种商品每个涨价1元,其销售量就减少10个,若这种商品涨价x元,则可赚得y元的利润.
(1)、写出x与y之间的关系式;
(2)、为了赚得8000元利润,售价应定为多少元,这时应进货多少个?
25. 如图,一次函数 的图象与反比例函数 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).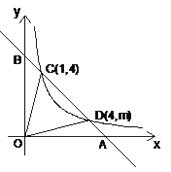 (1)、利用图中条件,求反比例函数的解析式和m的值;(2)、求△DOC的面积.(3)、双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
(1)、利用图中条件,求反比例函数的解析式和m的值;(2)、求△DOC的面积.(3)、双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.