浙江桐乡现代片四校2016-2017学年八年级上学期数学期中考试试卷
试卷更新日期：2018-11-21 类型：期中考试
一、单选题
-
1. 下列“QQ表情”中，属于轴对称图形的是 （ ）A、
B、
C、
D、
2. 下列句子是命题的是（ ）A、画∠AOB=45° B、小于直角的角是锐角吗？ C、连结CD D、三角形的中位线平行且等于第三边的一半3. 在下列各数中可以用来证明命题“质数一定是奇数”是假命题的反例是（ ）A、2 B、3 C、4 D、54. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）A、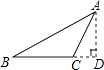
B、
C、
D、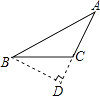
5. 等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（ ）A、12 B、15 C、12或15 D、186. 下列条件中，不能判定△ABC是直角三角形的是（ ）A、∠A：∠B：∠C=3：4：5 B、∠A ∠B= ∠C C、∠B=50°，∠C=40° D、a=5，b=12，c=137. 一个直角三角形的两直角边长分别为3和4，那么它斜边上的高线长为（ ）A、5 B、2.5 C、2.4 D、28. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝8，DE=4，则△BCE的面积等于（ ）
A、32 B、16 C、8 D、49. 如图所示的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，在网格中与△ABC成轴对称的格点三角形一共有（ ）
A、2个 B、3个 C、4个 D、5个10.如图，四边形ABCD是正方形，直线a，b，c分别通过A、D、C三点，且a∥b∥c．若a与b之间的距离是5，b与c之间的距离是7，则正方形ABCD的面积是（ ）
A、70 B、74 C、144 D、148二、填空题
-
11. 一个三边都是整数的三角形，其中两边长分别为1和2，第三边长是12. 命题“全等三角形的面积相等”的逆命题是（真或假）命题．13. 已知△ABC中，AB=AC=4，∠A=60度，则△ABC的周长为 ．14. 若等腰三角形的一个角为80°，则顶角为 ．15. 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则
A＝度。
16. 如图，在△ABC中，∠A=55°，∠B=60°，则外角∠ACD=度．
17. 如图，已知AC=DB，再添加一个适当的条件 ， 使△ABC≌△DCB．（只需填写满足要求的一个条件即可）．
18. 如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连结OC，若∠AOC=125°，则∠ABC=
19. 在直线l上依次摆放着七个正方形（如图）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1 ， S2 ， S3 ， S4 ， 则S1+S4= ．
20. 如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A1 ， B1 ， C1 ， 使A1B=AB、B1C=2BC，C1A=2CA，顺次连接A1 ， B1 ， C1 ， 得到△A1B1C1 ． 第二次操作：分别延长A1B1 ， B1C1、C1A1至点A2 ， B2 ， C2 ， 使A2B1=A1B1 ， B2C1=2B1C1 ， C2A1=2C1A1 ， 顺次连接A2 ， B2 ， C2 ， 得到△A2B2C2 ， …按此规律，经过2015次操作后△A2015B2015C2015的面积为 ．
三、解答题
-
21. 如图，已知AB=AC，AD=AE， ∠1=∠2，试说明BD=CE的理由.
22. 已知：如图，在△ABC中，∠BAC=80°，AD⊥BC于D，AE平分∠DAC，∠B=60°，求∠C、∠DAE的度数．
23. 如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E。求证△AED是等腰三角形．
24. 如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC．
(1)、求∠ECD的度数；
(2)、若CE=12，求BC长．25. 如图，在Rt△ABC中，∠ACB=90°．
(1)、用尺规在边BC上求作一点P，使PA=PB（不写作法，保留作图痕迹）；
(2)、连接AP，若AC=4，BC=8时，试求点P到AB边的距离．
26. 如图，已知△ABC中，∠B=90°，AB=8cm ， BC=6cm ， P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm ， 点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm ， 它们同时出发，设出发的时间为t秒．
(1)、出发2秒后，求PQ的长；
(2)、从几秒钟后，△PQB第一次能形成等腰三角形？
(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．