浙教版八年级下册第6章 6.2反比例函数的图像和性质 同步练习
试卷更新日期:2017-03-23 类型:同步测试
一、单选题
-
1. 对于函数y=﹣ , 下列结论错误的是( )A、当x>0时,y随x的增大而增大 B、当x<0时,y随x的增大而增大 C、当x=1时的函数值大于x=﹣1时的函数值 D、在函数图象所在的象限内,y随x的增大而增大2. 若反比例函数y=的图象经过点(2,﹣1),则该反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限3. 若A(1,y1),B(2,y2)两点都在反比例函数y= 的图象上,则y1与y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、无法确定4. 下列四个点,在反比例函数y= 的图像上的是( )A、(1,﹣6) B、(2,4) C、(3,﹣2) D、(﹣6,﹣1)5. 对于反比例函数y= (k≠0),下列说法不正确的是( )A、它的图像分布在第一、三象限 B、点(k,k)在它的图像上 C、它的图像关于原点对称 D、在每个象限内y随x的增大而增大6. 如图,函数y=k(x+1)与 (k<0)在同一坐标系中,图像只能是下图中的( )
A、 B、
B、 C、
C、 D、
D、 7. 如图,直线y=mx与双曲线y= 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为( )
7. 如图,直线y=mx与双曲线y= 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为( ) A、﹣2 B、2 C、4 D、﹣48. 若M(﹣2,y1),N(﹣1,y2),P(2,y3)三点都在函数y= (k<0)的图像上,则y1 , y2 , y3的大小关系是( )A、y3>y1>y2 B、y3>y2>y1 C、y1>y2>y3 D、y2>y1>y39. 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A、﹣2 B、2 C、4 D、﹣48. 若M(﹣2,y1),N(﹣1,y2),P(2,y3)三点都在函数y= (k<0)的图像上,则y1 , y2 , y3的大小关系是( )A、y3>y1>y2 B、y3>y2>y1 C、y1>y2>y3 D、y2>y1>y39. 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( ) A、y= B、y= C、y=﹣ D、y=﹣10. 如图,点P是x轴正半轴上的一动点,过点P作x轴的垂线,交双曲线y= 于点Q,连接OQ.当点P沿x轴的正方向运动时,Rt△QOP的面积( )
A、y= B、y= C、y=﹣ D、y=﹣10. 如图,点P是x轴正半轴上的一动点,过点P作x轴的垂线,交双曲线y= 于点Q,连接OQ.当点P沿x轴的正方向运动时,Rt△QOP的面积( ) A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定11. 如图,P为反比例函数y= 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图象上的是( )
A、逐渐增大 B、逐渐减小 C、保持不变 D、无法确定11. 如图,P为反比例函数y= 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图象上的是( ) A、(2,3) B、(﹣2,6) C、( 2,6 ) D、(﹣2,3)12. 关于反比例函数y=﹣ ,下列说法正确的是( )A、图像在第一、三象限 B、图像经过(2,1) C、在每个象限中,y随x的增大而减小 D、当x>1时,﹣2<y<013. 函数y=mx+n与y= ,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )A、
A、(2,3) B、(﹣2,6) C、( 2,6 ) D、(﹣2,3)12. 关于反比例函数y=﹣ ,下列说法正确的是( )A、图像在第一、三象限 B、图像经过(2,1) C、在每个象限中,y随x的增大而减小 D、当x>1时,﹣2<y<013. 函数y=mx+n与y= ,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )A、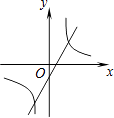 B、
B、 C、
C、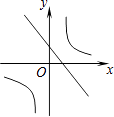 D、
D、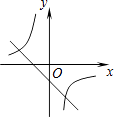 14. 如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ,则k的值是( )
14. 如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ,则k的值是( )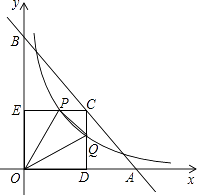 A、4 B、2 C、 D、15. 函数 y=ax2+a与 y= ( a≠0)在同一坐标系中的图象可能是图中的( )A、
A、4 B、2 C、 D、15. 函数 y=ax2+a与 y= ( a≠0)在同一坐标系中的图象可能是图中的( )A、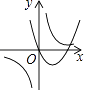 B、
B、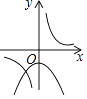 C、
C、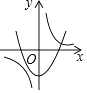 D、
D、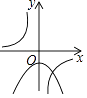
二、填空题
-
16. 反比例函数 ,在每个象限内,y随x的增大而增大,则m的取值范围是 .17. 反比例反数y=(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k= .
 18. 已知反比例函数y=﹣ , 则有
18. 已知反比例函数y=﹣ , 则有①它的图象在一、三象限:
②点(﹣2,4)在它的图象上;
③当l<x<2时,y的取值范围是﹣8<y<﹣4;
④若该函数的图象上有两个点A (x1 , y1),B(x2 , y2),那么当x1<x2时,y1<y2
以上叙述正确的是
19. 如图,点P、Q是反比例函数y= 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 20. 如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥y轴,C,D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .
20. 如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥y轴,C,D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .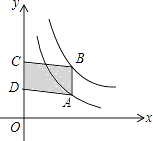
三、解答题
-
21. 如图,点A在双曲线y= (x>0)上,过点A作AC⊥x轴,垂足为C,线段OA的垂直平分线BD交x轴于点B,△ABC的周长为4,求点A的坐标.
 22. 已知反比例函数y=的图象经过点(﹣1,﹣2).
22. 已知反比例函数y=的图象经过点(﹣1,﹣2).(1)求y与x的函数关系式;
(2)若点(2,n)在这个图象上,求n的值
23. 如图,在正方形ABCD中,点A在y轴正半轴上,点B的坐标为(0,﹣3),反比例函数y=﹣的图象经过点C.(1)求点C的坐标;
(2)若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD;求点P的坐标.

