浙江省余姚市2017-2018学年八年级上学期数学期中考试试卷
试卷更新日期:2018-11-21 类型:期中考试
一、单选题
-
1. 下列汽车标志中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. △ABC中,∠A=40°,∠B=60°,则∠C的度数是( )A、40° B、60° C、80° D、100°3. 以下列各数为边长,能组成直角三角形的是( )A、3,4,5 B、4,5,6 C、5,6,7 D、7,8,94. 下列句子是命题的是( )A、画∠AOB=45° B、小于直角的角是锐角吗? C、连结CD D、三角形内角和等于180°5. 等腰三角形有两条边的长为4cm和9cm,则该三角形的周长( )A、17cm B、22cm C、17cm和22cm D、18cm6. 下列各图中,正确画出AC边上的高的是( )A、
2. △ABC中,∠A=40°,∠B=60°,则∠C的度数是( )A、40° B、60° C、80° D、100°3. 以下列各数为边长,能组成直角三角形的是( )A、3,4,5 B、4,5,6 C、5,6,7 D、7,8,94. 下列句子是命题的是( )A、画∠AOB=45° B、小于直角的角是锐角吗? C、连结CD D、三角形内角和等于180°5. 等腰三角形有两条边的长为4cm和9cm,则该三角形的周长( )A、17cm B、22cm C、17cm和22cm D、18cm6. 下列各图中,正确画出AC边上的高的是( )A、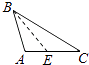 B、
B、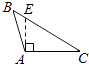 C、
C、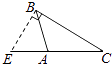 D、
D、 7. 已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形8. 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,D为BC的中点,EF=3,BC=8,则△DEF的周长是 ( )
7. 已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形8. 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,D为BC的中点,EF=3,BC=8,则△DEF的周长是 ( )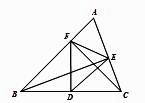 A、7 B、10 C、11 D、149. 勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A、7 B、10 C、11 D、149. 勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( ) A、90 B、100 C、110 D、121
A、90 B、100 C、110 D、121二、填空题
-
10. 如图,在△ABC中,点D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A的余角是 .
 11. 试写出命题“直角三角形的两个锐角互余”的逆命题: .12. 等腰三角形一腰上的中线将三角形的周长分成15和18,则这个等腰三角形的腰长 为 .
11. 试写出命题“直角三角形的两个锐角互余”的逆命题: .12. 等腰三角形一腰上的中线将三角形的周长分成15和18,则这个等腰三角形的腰长 为 .
13. 如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是16cm2 , 则阴影部分的面积等于cm2 . 14. 如图,AB=AC=4,∠A=45°,P为BC边上的一个动点,PD⊥AB于点 D,PE⊥AC于点E,则PE+PD= .
14. 如图,AB=AC=4,∠A=45°,P为BC边上的一个动点,PD⊥AB于点 D,PE⊥AC于点E,则PE+PD= .
三、解答题
-
15. 如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
 16. 已知:如图,直线AD与BC交于点O,OA=OD,OB=OC.求证:AB∥CD.
16. 已知:如图,直线AD与BC交于点O,OA=OD,OB=OC.求证:AB∥CD.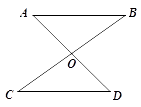 17. 已知:线段a,∠α.
17. 已知:线段a,∠α.求作:△ABC,使AB=BC=a,∠B=∠α.
 18. 如图,AC⊥BC,AD⊥BD,AD=BC,那么请你判断阴影部分图形的形状,并说明理由.
18. 如图,AC⊥BC,AD⊥BD,AD=BC,那么请你判断阴影部分图形的形状,并说明理由. 19. 在如图所示的网格中,每个小正方形的边长均为1个单位。
19. 在如图所示的网格中,每个小正方形的边长均为1个单位。 (1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形。(2)、请你在图2中画一条以格点为端点,长度为 的线段.
(1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形。(2)、请你在图2中画一条以格点为端点,长度为 的线段.
(3)、请你在图3中画一个以格点为顶点, 为直角边的直角三角形。20. 如图,△AED的顶点D在△ABC的BC边上,∠E=∠B,AE=AB, ∠EAB=∠DAC. (1)、求证:△AED≌△ABC.(2)、若∠E=40°,∠DAC=30°,求∠BAD的度数.
(1)、求证:△AED≌△ABC.(2)、若∠E=40°,∠DAC=30°,求∠BAD的度数.
21. 如图所示,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线.求证:AC+CD=AB.
 22. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点 P从点C开始,按C-A-B-C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
22. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点 P从点C开始,按C-A-B-C的路径运动,且速度为每秒1cm,设出发的时间为t秒. (1)、出发2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C-B-A-C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动
(1)、出发2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C-B-A-C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动 当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
当t为何值时,直线PQ把△ABC的周长分成相等的两部分?