2016-2017学年浙江省杭十五中教育集团九年级数学下学期3月学力检测试题卷

试卷更新日期：2017-03-23 类型：中考模拟

进入出卷网下载

一、选择题

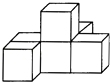
1. 下列各数中，是有理数是（）

A、 $\frac{22}{7}$ B、 $π$ C、 $\sqrt{2}$ D、 $\sqrt{5}$

查看试题解析
2. 当a= $\sqrt{2}$ ,b=1时，代数式(a+2b)(a-2b)的值为（）

A、3 B、0 C、 -1 D、-2

查看试题解析
3. 如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 某校有25名同学参加某比赛，预赛成绩各不相同，取前13名参加决赛，其中一名同学已经知道自己的成绩，能否进入决赛，只需要再知道这25名同学成绩的（）

A、最高分 B、平均数 C、中位数 D、方差

查看试题解析
5.
如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）为4m．如果在坡比为 $i = 3 ： 4$ 的山坡上种树，也要求株距为4m，那么相邻两树间的坡面距离为（）

A、5m B、6m C、7m D、8m

查看试题解析
6. 下列计算正确的是（）

A、x⁴+x⁴=2x⁸ B、x³•x²=x⁶ C、（x²y）³=x⁶y³ D、（x﹣y）⁶÷（y﹣x）³=（x﹣y）³

查看试题解析
7. 下列命题为假命题的个数有（）
① 相等的角是对顶角；
② 依次连结四边形四边中点所组成的图形是平行四边形；
③ 在同圆或等圆中，相等的弦所对的圆周角相等；
④ 在同圆中，平分弦的直径垂直于这条弦。

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 对于反比例函数 $y = \frac{k}{x}$ ，如果当 $- 2$ ≤ $x$ ≤ $- 1$ 时有最大值 $y = 4$ ，则当 $x$ ≥8时，有（）

A、最大值 $y = - 1$ B、最小值 $y = - 1$ C、最大值y= $- \frac{1}{2}$ D、最小值y= $- \frac{1}{2}$

查看试题解析
9.
如图，⊙O的半径为2，AB，CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A，B，C，D不重合），过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为（）

A、 $\frac{π}{2}$ B、 $\frac{π}{3}$ C、 $\frac{π}{4}$ D、 $\frac{π}{6}$

查看试题解析
10.
如图，直线l₁∥l₂∥l₃ ，等腰Rt△ABC的三个顶点A，B，C分别在l₁ ， l₂ ， l₃上，∠ ACB=90°，AC交l₂于点D，已知l₁与l₂的距离为1，l₂与l₃的距离为3，则AB：BD的值为（）

A、 $\frac{4}{5} \sqrt{2}$ B、 $\frac{\sqrt{34}}{5}$ C、 $\frac{5}{8} \sqrt{2}$ D、 $\frac{3}{20} \sqrt{2}$

查看试题解析

二、填空题

11. G20峰会于9月4日至5日在浙江杭州召开，主会场场馆规划总建筑面积1302万平方米。1302万用科学记数法可表示为平方米。

查看试题解析
12.
如图，AB∥CD，以点B为圆心，小于DB长为半径作圆弧，分别交BA、BD于点E、F，再分别以点E、F，为圆心，大于 $\frac{1}{2} E F$ 长为半径作圆弧，两弧交于点G，作射线BG交CD于点H。若∠D=116°，则∠DHB的大小为°。

查看试题解析
13. 对于平面图形上的任意两点P，Q，如果经过某种变换（如：平移、旋转、轴对称等）得到新图形上的对应点P′，Q′，保持P P′= Q Q′，我们把这种对应点连线相等的变换称为“同步变换”。对于三种变换： ①平移、②旋转、③轴对称，其中一定是“同步变换”的有（填序号）。

查看试题解析
14. 若关x的函数y＝kx²＋2x－1的图像与x轴仅有一个交点，则实数k的值为。

查看试题解析
15.
如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则正方形MNPQ与正方形AEFG的面积之比等于。

查看试题解析
16. 有下列四个结论：
①a÷m+a÷n=a÷(m+n)；
② 某商品单价为a元。甲商店连续降价两次，每次都降10%。乙商店直接降20%。顾客选择甲或乙商店购买同样数量的此商品时，获得的优惠是相同的；
③若 $x^{2} + y^{2} + 2 x - 4 y + 5 = 0$ ，则 $y^{x}$ 的值为 $\frac{1}{2}$ ；
④关于x分式方程 $\frac{2 x - a}{x - 1} = 1$ 的解为正数，则 $a$ ＞1。
请在正确结论的题号后的空格里填“正确” ，在错误结论的题号后空格里填“错误”：
①； ②； ③； ④

查看试题解析

三、解答题

17. 按要求完成化简：

(1)、计算与化简： $\cos 60^{\circ} \cdot \tan 30^{\circ}$

(2)、因式分解： $3 a^{2} - 6 a + 3$

查看试题解析
18.
我校对全部900名学生就校园安全知识的了解程度，采用随机抽样调查的方式进行调查，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

(1)、接受问卷调查的学生共有人，条形统计图中“了解”部分所对应的人数是人；

(2)、扇形统计图中“基本了解”部分所对应扇形的圆心角为°；

(3)、若没有达到“了解”或“基本了解”的同学必须重新接受安全教育。请根据上述调查结果估计我校学生中必须重新接受安全教育的总人数大约为人；

(4)、若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请直接写出恰好抽到1个男生和1个女生的概率。

查看试题解析
19.
用如图（1）中的长方形和正方形纸板作侧面和底面，做成如图（2）所示的竖式和横式两种无盖纸盒。现仓库里有1000张正方形纸板和2000张长方形纸板，问两种纸盒各做多少个，恰好将库存纸板用完？

查看试题解析
20.
如图，B、C、D在同一直线上，△ABC和△DCE都是等边三角形，且在直线BD的同侧，BE交AD于F，BE交AC于M，AD交CE于N.

(1)、求证：AD=BE；

(2)、求证：△ABF∽△ADB。

查看试题解析
21.
如图，在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），双曲线y= $\frac{k}{x}$ （k≠0，x＞0）过点D．

(1)、求此双曲线的解析式；

(2)、作直线AC交y轴于点E，连结DE，求△ CDE的面积．

查看试题解析
22.
如图，△ABC中，AB=AC=10，BC= $4 \sqrt{5}$ ，以AB为直径的⊙O分别交BC、AC于点D、E.

(1)、求AE；

(2)、过D作DF⊥AC于F，请画出图形，说明DF是否是⊙O的切线，并写出理由；

(3)、延长FD，交AB的延长线于G，请画出图形，并求BG.

查看试题解析
23.
如图，已知点A（0，2），B（2，2），C（－1，－2），抛物线F： $y = x^{2} - 2 m x + m^{2} - 2$ 与直线x=－2交于点P.

(1)、当抛物线F经过点C时，求它的表达式；

(2)、抛物线F上有两点M $(x_{1} ， y_{1})$ 、N $(x_{2} ， y_{2})$ ，若－2≤ $x_{1} < x_{2}$ ， $y_{1}$ ＜ $y_{2}$ ，求m的取值范围；

(3)、设点P的纵坐标为 $y_{P}$ ，求 $y_{P}$ 的最小值，此时抛物线F上有两点M $(x_{1} ， y_{1})$ 、N $(x_{2} ， y_{2})$ ，
若 $x_{1} < x_{2}$ ≤－2，比较 $y_{1}$ 与 $y_{2}$ 的大小；

(4)、当抛物线F与线段AB有公共点时，直接写出m的取值范围。

查看试题解析