湖北省宜昌市2018-2019学年度上学期人教版9年级数学期末测试卷

试卷更新日期：2018-11-21 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 5 x - 6 = 0$ 的根是（）

A、 $x_{1} = 1$ ， $x_{2} = 6$ B、 $x_{1} = 2$ ， $x_{2} = 3$ C、 $x_{1} = 1$ ， $x_{2} = - 6$ D、 $x_{1} = - 1$ ， $x_{2} = 6$

查看试题解析
2. 抛物线y=2（x﹣5）²+3的顶点坐标是（）

A、（5，3） B、（﹣5，3） C、（5，﹣3） D、（﹣5，﹣3）

查看试题解析
3. 二次函数y=x²﹣6x﹣7的对称轴为（）

A、x=3 B、x=﹣3 C、x=﹣1 D、x=7

查看试题解析
4. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、等边三角形 B、干行四边形 C、正六边形 D、圆

查看试题解析
5. 若方程x²﹣4x+c=0有两个不相等的实数根，则实数c的值可以是（）

A、6 B、5 C、4 D、3

查看试题解析
6. 如图，将线段AB绕点O顺时针旋转90°得到线段A'B'，那么A(－2，5)的对应点A′的坐标是（）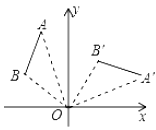

A、(2，5) B、(5， 2) C、(2，－5) D、(5，－2)

查看试题解析
7. 已知x=2是一元二次方程x²﹣mx﹣10=0的一个根，则m等于（）

A、﹣5 B、5 C、﹣3 D、3

查看试题解析
8. 如图，AB是⊙O的弦，半径OC⊥AB于点D，若⊙O的半径为5，AB=8，则CD的长是（）

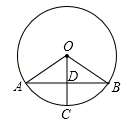A、2 B、3 C、4 D、5

查看试题解析
9. 二次函数y＝x²－2x－3的图象如图所示，当y<0时，自变量x的取值范围是（）

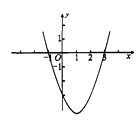A、－1<x<3 B、x<－1 C、x>3 D、x<－3或x>3

查看试题解析
10. 下列事件中，属于必然事件的是 $($ )

A、三角形的外心到三边的距离相等 B、某射击运动员射击一次，命中靶心 C、任意画一个三角形，其内角和是 $180^{\circ}$ D、抛一枚硬币，落地后正面朝上

查看试题解析
11. 小明随机地在如图所示的正三角形及其内部区域投针，则针扎到其内切圆（阴影）区域的概率为（）

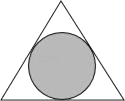A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{6} π$ C、 $\frac{\sqrt{3}}{9} π$ D、 $\frac{3 \sqrt{3}}{π}$

查看试题解析
12. 如图，已知：在⊙O中，OA⊥BC，∠AOB=70°，则∠ADC的度数为（）

A、70° B、45° C、35° D、30°

查看试题解析
13. 如图，AB为半圆O的直径，C为AO的中点，CD⊥AB交半圆于点D，以C为圆心，CD为半径画弧交AB于E点，若AB＝4，则图中阴影部分的面积是（）

A、 $\frac{7}{12} π + \frac{\sqrt{3}}{2}$ B、 $\frac{5}{12} π$ C、 $\frac{7}{12} π - \frac{\sqrt{3}}{2}$ D、 $\frac{2}{3} π$

查看试题解析
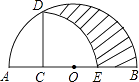14. 已知：抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
①4ac＜b²；②方程ax²+bx+c=0的两个根是x₁=﹣1，x₂=3；
③a﹣b+c＞0；④当y＞0时，x的取值范围是﹣1≤x＜3；
⑤当x＜0时，y随x增大而增大
其中正确的结论有（）

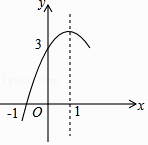A、4个 B、3个 C、2个 D、1个

查看试题解析
15. 二次函数y=ax²+bx+c的图象如图所示，对称轴是直线x=﹣1，有以下结论：①abc＞0；②4ac＜b²；③2a+b=0；④a﹣b+c＞2．其中正确的结论的个数是（）

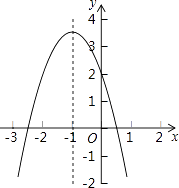A、1 B、2 C、3 D、4

查看试题解析

二、解答题

16. 解方程：

(1)、（x+3）²=2x+6；

(2)、x²﹣2x=8．

查看试题解析
17. 已知关于 $x$ 的方程 $x^{2} + (m + 2) x + 2 m - 1 = 0$ .

(1)、求证：方程有两个不相等的实数根.

(2)、当 $m$ 为何值时，方程的两根互为相反数？并求出此时方程的解.

查看试题解析
18. 在北京2008年第29届奥运会前夕，某超市在销售中发现：奥运会吉祥物— “福娃”平均每天可售出20套，每件盈利40元。为了迎接奥运会，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存。经市场调查发现：如果每套降价4元，那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元，那么每套应降价多少？

查看试题解析
19. 如图，在圆内接四边形ABCD中，O为圆心，∠BOD=160°，求∠BCD的度数．

查看试题解析
20. 如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B出发，以 $\sqrt{3}$ cm/s的速度沿BC方向
运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA-AC方向运动到点C停止，若△BPQ的面积为y（cm²），运动时间为x（s），求在这一运动过程中y与x之间函数关系式.

查看试题解析
21. 甲、乙两人分别站在相距6米的A、B两点练习打羽毛球，已知羽毛球飞行的路线为抛物线的一部分，甲在离地面1米的C处发出一球，乙在离地面1.5米的D处成功击球，球飞行过程中的最高点H与甲的水平距离AE为4米，现以A为原点，直线AB为x轴，建立平面直角坐标系（如图所示）．求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度．

查看试题解析
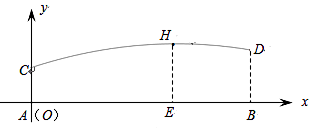22. 如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．

查看试题解析
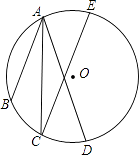23. 已知抛物线y=（x﹣m）²﹣（x﹣m），其中m是常数．

(1)、求证：不论m为何值，该抛物线与x轴一定有两个公共点；

(2)、若该抛物线的对称轴为直线x= $\frac{5}{2}$ ．
①求该抛物线的函数解析式；
②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有一个公共点．

查看试题解析
24.
如图，⨀C的内接△AOB中，AB=AO=4，tan∠AOB= $\frac{3}{4}$ ，抛物线y=ax²+bx经过点A（4，0）与点（-2，6）.

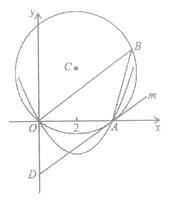(1)、求抛物线的函数解析式；

(2)、直线m与⨀C相切于点A，交y轴于点D，求证：AD//OB；

(3)、在（2）的条件下，点P在线段OB上，从点O出发向点B运动；同时动点Q在线段DA上，从点D出发向点A运动；点P的速度为每秒1个单位长，点Q的速度为每秒2个单位长，当PQ⊥AD时，求运动时间t的值.

查看试题解析