浙教版八年级下册第5章 5.3正方形 同步练习
试卷更新日期：2017-03-23 类型：同步测试
一、单选题
-
1. 一个正方形的边长为3，则它的对角线长为（ ）A、3 B、3 C、 D、22. 如图，正方形ABCD中，以对角线AC为一边作菱形AEFC，则∠FAB等于（ ）
A、22.5° B、45° C、30° D、135°3. 如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上．下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+ ．其中正确的个数为（ ）
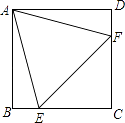A、1 B、2 C、3 D、44. 如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（ ）
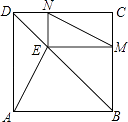
A、16 B、12 C、8 D、45. 如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点当PC+PD最小时，∠PCD=（ ）°．
A、60° B、45° C、30° D、15°6. 观察如图，把边长为3的两个正方形沿其对角线长剪开，可得4个直角三角形，这4个直角三角形可拼成一个新的正方形，则新正方形的边长为（ ）
A、3 B、6 C、 D、187. 如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB，BD于M，N两点．若AM=2，则线段ON的长为（ ）
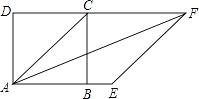
A、 B、 C、1 D、8.将n个边长都为1cm的正方形按如图所示的方法摆放，点A1 ， A2 ， …，An分别是正方形对角线的交点，则n个正方形重叠形成的重叠部分的面积和为（ ）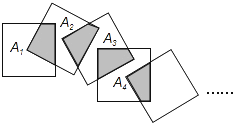
A、cm2 B、cm2 C、cm2 D、（ ）ncm29. 正方形面积为36，则对角线的长为（ ）A、6 B、6 C、9 D、910. 在平面中，下列说法正确的是（ ）A、四边相等的四边形是正方形 B、四个角相等的四边形是矩形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形11. 将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B=90°时，如图1，测得AC=2，当∠B=60°时，如图2，AC=（ ）
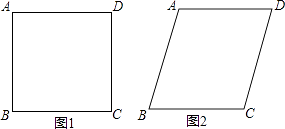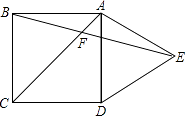
A、 B、2 C、 D、212.如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（ ）
A、45° B、55° C、60° D、75°13. 如图，在四边形ABCD的外侧，以四边形的边为边分别作四个小正方形，连接相邻的两个顶点，得到四个阴影三角形，则这四个阴影三角形的面积a、b、c、d满足（ ）
A、a+b=c+d B、a2+b2=c2+d2 C、a+c=b+d D、a2+c2=b2+d214.如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：（1）AE=BF；（2）AE⊥BF；（3）AO=OE；（4） 中正确的有（ ）
A、 4个 B、 3个 C、 2个 D、 1个二、填空题
-
15.
如图，点E、F分别为正方形ABCD中AB、BC边的中点，连接AF、DE相交于点G，连接CG，则tan∠CGD=
16.如图，由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”，其中阴影部分面积为 ．
17.已知，如图，四边形ABCD是正方形，BE=AC，则∠BED=度．
18. 如图，正方形ABCD的边长为4，点P在DC边上且DP=1，点Q是AC上一动点，则DQ+PQ的最小值为 ．
19. 如图，在等边△ABC的外侧作正方形ABDE，AD与CE交于F，则∠ABF的度数为 ．
三、综合题
-
20. 已知，如图，正方形ABCD的对角线AC，BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，A′B′交BC于点E，A′D′交CD于点F．
(1)、求证：OE=OF；(2)、若正方形ABCD的对角线长为4，求两个正方形重叠部分的面积为21. 如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．
(1)、求证：CE=CF；(2)、若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？22.如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．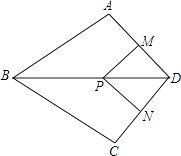
(1)、求证：∠ADB=∠CDB；(2)、若∠ADC=90°，求证：四边形MPND是正方形．
