浙教版八年级下册第5章 5.2菱形 同步练习
试卷更新日期：2017-03-23 类型：同步测试
一、单选题
-
1. 已知菱形的周长为40cm，两条对角线之比3：4，则菱形面积为（ ）A、962 B、48cm2 C、24cm2 D、12cm22. 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）
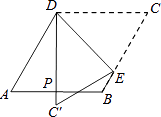A、78° B、75° C、60° D、45°3. 如图，在菱形ABCD中，AB=8，点E，F分别在AB，AD上，且AE=AF，过点E作EG∥AD交CD于点G，过点F作FH∥AB交BC于点H，EG与FH交于点O．当四边形AEOF与四边形CGOH的周长之差为12时，AE的值为（ ）
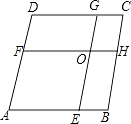A、6.5 B、6 C、5.5 D、54. 如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD，则四边形ABCD面积的最大值是（ ）
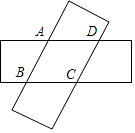A、15 B、16 C、19 D、205.如图四边形ABCD是菱形，对角线AC=8，BD=6，DH⊥AB于点H，则DH的长度是（ ）
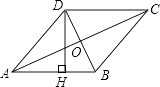A、 B、 C、 D、6.如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，则菱形ABCD的周长是（ ）
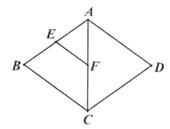A、12 B、16 C、20 D、247. 如图，正方形ABCD中，以对角线AC为一边作菱形AEFC，则∠FAB等于（ ）
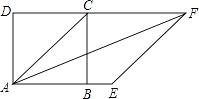A、22.5° B、45° C、30° D、135°8. 如图，下列选项中能使平行四边形ABCD是菱形的条件有（ ）①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD．
A、①③ B、②③ C、③④ D、①②③9. 菱形具有而矩形不具有的性质是（ ）A、对角线互相平分 B、四条边都相等 C、对角相等 D、邻角互补10. 菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（ ）A、3：1 B、4：1 C、5：1 D、6：111. 菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线的长度是（ ）A、20 B、5 cm C、 cm D、5cm12. 下列命题中，是真命题的是（ ）A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形13.如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形CODE的周长（ ）
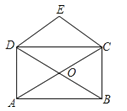A、4 B、6 C、8 D、1014. 如图，在菱形ABCD中，AB=10，对角线AC=12．若过点A作AE⊥CD，垂足为E，则AE的长为（ ）
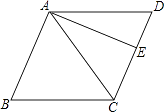A、9 B、 C、 D、9.515. 如图，已知四边形ABCD是菱形，过顶点D作DE⊥AD，交对角线AC于点E，若∠DAE=20°，则∠CDE的度数是（ ）
A、70° B、60° C、50° D、40°二、填空题
-
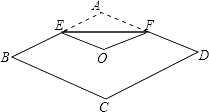
16. 已知一个菱形的面积为8 cm2 ， 且两条对角线的长度比为1： ，则菱形的边长为 ．17.
如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF，若菱形ABCD的边长为2cm，∠A=120°，则EF=cm．
18. 如图，ABCD是对角线互相垂直的四边形，且OB=OD，请你添加一个适当的条件 ， 使ABCD成为菱形（只需添加一个即可）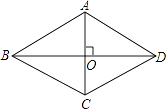
19. 如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为 ．
20. 如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是 ．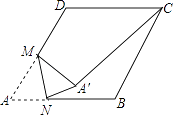
三、综合题
-
21. 如图，AE∥BF，AC平分∠BAD，交BF于点C，BD平分∠ABC，交AE于点D，连接CD．
(1)、若AB=1，则BC的长=；(2)、求证：四边形ABCD是菱形．22. 已知：如图，菱形花坛ABCD周长是80m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD，相交于O点．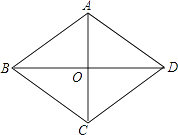
(1)、求两条小路的长AC、BD．（结果可用根号表示）(2)、求花坛的面积．（结果可用根号表示）23. 如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）．
(1)、连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF；(2)、填空：①当t为 s时，四边形ACFE是菱形；
②当t为 s时，以A、F、C、E为顶点的四边形是直角梯形．
四、解答题
-
24. 如图，CE是△ABC外角∠ACD的平分线，AF∥CD交CE于点F，FG∥AC交CD于点G．求证：四边形ACGF是菱形．
