2019年高考（文科）数学模拟测试卷（新课标3卷）

试卷更新日期：2018-11-20 类型：高考模拟

进入出卷网下载

一、单选题

1. 若集合M={﹣2，﹣1，0，1，2}，N={x|x²＜3}，则M∩N等于（　　）

A、∅ B、{﹣1，1} C、{﹣2，2} D、{﹣1，0，1}

查看试题解析
2. 已知 $i$ 是虚数单位，若复数 $(1 + a i) (2 + i)$ 是纯虚数，则实数 $a$ 等于 ( )

A、 $2$ B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $- 2$

查看试题解析
3. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 为棱 $B B_{1}$ 的中点，用过点 $A$ ， $E$ ， $C_{1}$ 的平面截去该正方体的上半部分，则剩余几何体的左(侧)视图为（）

A、 B、 C、 D、

查看试题解析
4. 若 $x \in (- \frac{3}{4} π ， \frac{π}{4})$ 且 $\cos (\frac{π}{4} - x) = - \frac{3}{5}$ 则cos2x的值是（　　）

A、 $- \frac{7}{25}$ B、 $- \frac{24}{25}$ C、 $\frac{24}{25}$ D、 $\frac{7}{25}$

查看试题解析
5. 从一箱产品中随机地抽取一件，设事件A={抽到一等品}，事件B={抽到二等品}，事件C={抽到三等品}，且已知P（A）=0.7，P（B）=0.2，P（C）=0.1．则事件“抽到的不是一等品”的概率为（　　）

A、0.7 B、0.2 C、0.1 D、0.3

查看试题解析
6. 下列函数中，最小正周期 $π$ 为且图象关于原点对称的函数是（）

A、y=cos(2x+ $\frac{π}{2}$ ) B、y=sin(2x+ $\frac{π}{2}$ ) C、y=sin2x+cos2x D、y=sinx+cosx

查看试题解析
7. 函数 $f (x) = \frac{1}{x} - x$ 的图象关于（）

A、y轴对称 B、坐标原点对称 C、直线y=x对称 D、直线y=﹣x对称

查看试题解析
8. 设 $m ， n \in R$ ，若直线 $l ： m x + n y - 1 = 0$ 与 $x$ 轴相交于点 $A$ ，与 $y$ 轴相交于点B，且坐标原点O到直线 $l$ 的距离为 $\sqrt{3}$ ，则 $△ A O B$ 的面积 $S$ 的最小值为( )

A、 $\frac{1}{2}$ B、2 C、3 D、4

查看试题解析
9. 已知函数f（x）=ln|ax|（a≠0），g（x）=x^﹣³+sinx，则（）

A、f（x）+g（x）是偶函数 B、f（x）•g（x）是偶函数 C、f（x）+g（x）是奇函数 D、f（x）•g（x）是奇函数

查看试题解析
10. 过双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点F，作渐近线 $y = \frac{b}{a} x$ 的垂线与双曲线左右两支都相交，则双曲线的离心率e的取值范围为 ( )

A、 $1 < e < 2$ B、 $1 < e < \sqrt{2}$ C、 $e > \sqrt{2}$ D、 $e > 2$

查看试题解析
11. 若 $△ A B C$ 的内角A，B，C所对的边a，b，c满足 ${(a + b)}^{2} - c^{2} = 4$ ，且 $C = 60^{\circ}$ ，则 ab的值为（　　）

A、 $8 - 4 \sqrt{3}$ B、11 C、 $\frac{4}{3}$ D、 $\frac{2}{3}$

查看试题解析
12. 由8个面围成的几何体，每个面都是正三角形，并且有四个顶点A，B，C，D在同一平面上，ABCD是边长为15的正方形，则该几何体的外接球的体积为（）

A、1125 $\sqrt{2}$ π B、3375 $\sqrt{2}$ π C、450π D、900π

查看试题解析

二、填空题

13. 设向量 $\vec{a}$ =（1，﹣4）， $\vec{b}$ =（﹣1，x）， $\vec{c}$ =（ $\vec{a}$ +3 $\vec{b}$ ），若 $\vec{a}$ ∥ $\vec{c}$ ，则实数x的值为．

查看试题解析
14. 某小学三个年级共有学生270人，其中一年级108人，二、三年级各81人，现要用抽样方法抽取10人形成样本，将学生按一、二、三年级依次统一编号为1,2，……，270，如果抽得号码有下列四种情况：
①5,9,100,107,111,121,180,195,200,265；
②7,34,61,88,115,142,，169,196，223,250；
③30,57,84,111,138，165,192,219,246,270；
④11,38,60,90,119,146,173,200,227，254.
其中可能是由分层抽样得到，而不可能是由系统抽样得到的一组号码为．（填序号）

查看试题解析
15. 设变量x，y满足约束条件 ${\begin{matrix} y \leq x \\ x + y \geq 2 \\ y \geq 3 x - 6 \end{matrix}$ ，则目标函数z=2x+y的最小值为．

查看试题解析
16. 设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x+2）=﹣f（x）．当x∈[0，2]时，f（x）=2x﹣x² ．当x∈[2，4]时，则f（x）= ．

查看试题解析

三、解答题

17. 在公差为d的等差数列{a_n}中，已知a₁=10，且a₁ ， 2a₂+2，5a₃成等比数列．

(1)、求d，a_n；

(2)、若d＜0，求|a₁|+|a₂|+|a₃|+…+|a_n|．

查看试题解析
18. 某品牌经销商在一广场随机采访男性和女性用户各50名，其中每天玩微信超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如下：

微信控
非微信控
合计
男性
26
24
50
女性
30
20
50
合计
56
44
100
参考公式： $k^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
参考数据：
$P (K^{2} \geq k_{0})$
0.50
0.40
0.25
0.15
0.10
0.05
0.025
$k_{0}$
0.455
0.708
1.323
2.072
2.706
3.841
5.024

(1)、根据以上数据，能否有95%的把握认为“微信控”与“性别”有关？

(2)、现从调查的女性用户中按分层抽样的方法选出5人，求所抽取的5人中“微信控”和“非微信控”的人数；

(3)、从（2）中抽取的5位女性中，再随机抽取3人赠送礼品，试求抽取3人中恰有2人位“微信控”的概率.

查看试题解析
19. 如图所示，在四棱锥 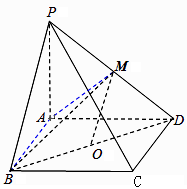$P-ABCD$ 中，已知 $PA ⊥ 底面 ABCD$ 底面 $A B C D$ 是矩形， $O$ 是 $B D$ 的中点， $P A = A D$ .

(1)、在线段 $P D$ 上找一点 $M$ ，使得 $OM ∥ 平面 PAB$ ，并说明理由；

(2)、在（1）的条件下，求证 $平面 ABM ⊥ 平面 PCD$ .

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{6}}{3}$ ，直线l：x+y﹣1=0与C相交于A，B两点．

(1)、证明：线段AB的中点为定点，并求出该定点坐标；

(2)、设M（1，0）， $\vec{M A} = λ \vec{B M}$ ，当 $a \in (\frac{\sqrt{7}}{2} ， \sqrt{3})$ 时，求实数λ的取值范围．

查看试题解析
21. 已知函数f（x）= $\frac{x}{l n x} ， g (x) = k (x - 1)$ ．

(1)、证明：∀k∈R，直线y=g（x）都不是曲线y=f（x）的切线；

(2)、若∃x∈[e，e²]，使得f（x）≤g（x）+ $\frac{1}{2}$ 成立，求实数k的取值范围．

查看试题解析
22. 在直角坐标系 $x o y$ 中，直线 $l$ 的参数方程为 ${\begin{cases} x = 1 - \frac{\sqrt{2}}{2} t \\ y = 4 - \frac{\sqrt{2}}{2} t \end{cases}$ （ $t$ 为参数）．再以原点为极点，以 $x$ 正半轴为极轴建立极坐标系，并使得它与直角坐标系 $x o y$ 有相同的长度单位．在该极坐标系中圆 $C$ 的方程为 $ρ = 4 sin θ$ ．

(1)、求圆 $C$ 的直角坐标方程；

(2)、设圆 $C$ 与直线 $l$ 交于点 $A$ 、 $B$ ，若点 $M$ 的坐标为 $(1 ， 4)$ ，求 $| M A | + | M B |$ 的值．

查看试题解析
23. 设函数，f（x）=|x﹣a|
（Ⅰ）当a=2，解不等式，f（x）≥5﹣|x﹣1|；
（Ⅱ）若f（x）≤1的解集为[0，2]， $\frac{1}{m}$ + $\frac{1}{2 n}$ =a（m＞0，n＞0），求证：m+2n≥4．

查看试题解析

	微信控	非微信控	合计
男性	26	24	50
女性	30	20	50
合计	56	44	100

$P (K^{2} \geq k_{0})$	0.50	0.40	0.25	0.15	0.10	0.05	0.025
$k_{0}$	0.455	0.708	1.323	2.072	2.706	3.841	5.024