浙江省杭州市2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2018-11-20 类型:期中考试
一、选择题
-
1. 随机掷两枚硬币,落地后全部正面朝上的概率是( )A、1 B、 C、 D、2. 已知二次函数y=ax2+bx-1(a≠0)的图象经过点(2,4),则代数式1﹣2a﹣b的值为( )A、-4 B、- C、 D、3. 以下四个命题中属于假命题的是( )A、直径是弦 B、过三点一定可以作一个圆 C、半径相等的两个半圆是等弧 D、圆既是轴对称图形,又是中心对称图形4. 抛物线y= - (x-4)2+1与坐标轴的交点个数是( )
A、0个 B、1个 C、2个 D、3个5. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( ) A、点P B、点Q C、点R D、点M6. 如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等( )
A、点P B、点Q C、点R D、点M6. 如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等( )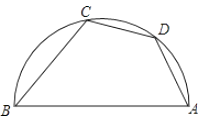 A、55° B、60° C、65° D、70°7. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象是( )A、
A、55° B、60° C、65° D、70°7. 在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象是( )A、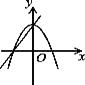 B、
B、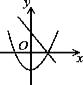 C、
C、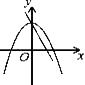 D、
D、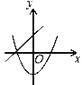 8. 一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球,两次都摸到红球的概率为( )A、 B、 C、 D、9. 如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )
8. 一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球,两次都摸到红球的概率为( )A、 B、 C、 D、9. 如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为( )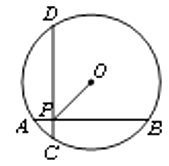 A、3 B、4 C、3 D、410. 已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0 , y0)是该抛物线的顶点,若y1>y2≥y0 , 则x0的取值范围是( )A、x0>-5 B、x0>-1 C、-5<x0<-1 D、-2<x0<3
A、3 B、4 C、3 D、410. 已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0 , y0)是该抛物线的顶点,若y1>y2≥y0 , 则x0的取值范围是( )A、x0>-5 B、x0>-1 C、-5<x0<-1 D、-2<x0<3二、填空题
-
11. 两直角边长分别为6和8的直角三角形的外接圆直径是 .
12. 如图,在圆O中,AB=AC,∠A=30°,则∠B= . 13. 抛物线y=-x2向左平移1个单位,再向上平移2个单位,则平移后抛物线的函数表达式是 .
13. 抛物线y=-x2向左平移1个单位,再向上平移2个单位,则平移后抛物线的函数表达式是 .
14. 若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上的数字为6,则从3,4,5,7,8中任选两数(不重复),与6组成“中高数”的概率是为 .
15. 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-1,0),B(4,0),则函数y=(kx+b),y=(mx+n)中,当y<0时x的取值范围是 .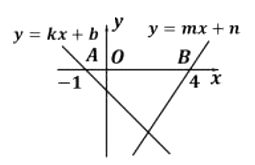 16. 如图,AB、CD为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF折叠,使B与圆心M重合,折痕EF与AB相交于N,连结AE、AF,得到了以下结论:①四边形MEBF是菱形,②△AEF为等边三角形,③S△AEF∶S圆=3 ∶4π,其中正确的是 .
16. 如图,AB、CD为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF折叠,使B与圆心M重合,折痕EF与AB相交于N,连结AE、AF,得到了以下结论:①四边形MEBF是菱形,②△AEF为等边三角形,③S△AEF∶S圆=3 ∶4π,其中正确的是 .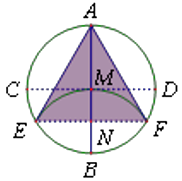
三、解答题
-
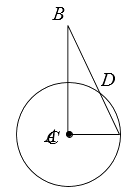
17. 如图,在△ABC中,∠ACB=90°,∠B=25°,CA=3,以点C为圆心,CA长为半径的圆交AB于点D,求弧AD的长。
 18. 如图某野生动物园分A、B两个园区.下图是该动物园的通路示意图,小明进入入口后,任选一条通道.
18. 如图某野生动物园分A、B两个园区.下图是该动物园的通路示意图,小明进入入口后,任选一条通道.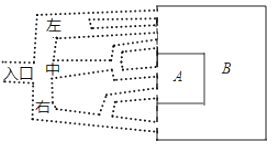 (1)、他进A园区或B园区的可能性哪个大?请说明理由(利用树状图或列表来求解);(2)、求小明从中间通道进入A园区的概率19. 已知等边三角形ABC.
(1)、他进A园区或B园区的可能性哪个大?请说明理由(利用树状图或列表来求解);(2)、求小明从中间通道进入A园区的概率19. 已知等边三角形ABC.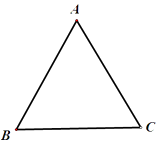 (1)、用尺规作图找出△ABC外心O.(2)、记外心O到三角形三边的距离和为d,到三角形三个顶点的距离和为D,求 的值20. 如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称.已知一次函数y=kx+b的图象经过该二次函数图象上的点A(-1,0)及点B.
(1)、用尺规作图找出△ABC外心O.(2)、记外心O到三角形三边的距离和为d,到三角形三个顶点的距离和为D,求 的值20. 如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称.已知一次函数y=kx+b的图象经过该二次函数图象上的点A(-1,0)及点B.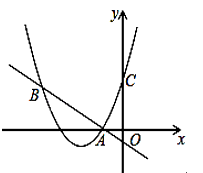 (1)、求二次函数与一次函数的表达式.
(1)、求二次函数与一次函数的表达式.
(2)、根据图象,写出满足(x+2)2≥kx+b-m的x的取值范围
21. 如图,AB是⊙O的直径,C是BD的中点,CE⊥AB于E,BD交CE于点F.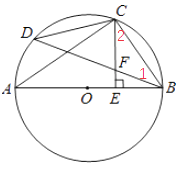 (1)、求证:CF=BF;(2)、若CD=6,AC=8,求⊙O的半径和CE的长.
(1)、求证:CF=BF;(2)、若CD=6,AC=8,求⊙O的半径和CE的长.
