湖南省邵阳市邵东县2018—2019学年上学期九年级数学第四章单元测试卷

试卷更新日期：2018-11-20 类型：单元试卷

进入出卷网下载

一、单选题

1. 2cos60°=（）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 在Rt△ABC中，∠C=90°，AC=4，cosA的值等于 $\frac{3}{5}$ ，则AB的长度是（）

A、3 B、4 C、5 D、 $\frac{20}{3}$

查看试题解析
3. 把Rt△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦函数值（）

A、不变 B、缩小为原来的 $\frac{1}{3}$ C、扩大为原来的3倍 D、不能确定

查看试题解析
4. 已知在Rt△ABC中，∠C=90°，AB=7，BC=5，那么下列式子中正确的是（）

A、 $sin A = \frac{5}{7}$ B、 $cos A = \frac{5}{7}$ C、 $tan A = \frac{5}{7}$ D、 $cot A = \frac{5}{7}$

查看试题解析
5. 在 $Δ A B C$ 中， $∠ C =90°$ ，若cosB= $\frac{\sqrt{3}}{2}$ ，则sinA的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 如图，要测量小河两岸相对的两点P，A的距离，可以在小河边取PA的垂线PB上的一点C，测得PC=100米，∠PCA=35°，则小河宽PA等于（）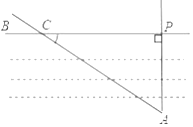

A、100sin35°米 B、100sin55°米 C、100tan35°米 D、100tan55°米

查看试题解析
7. 如图，滑雪场有一坡角α为20°的滑雪道，滑雪道AC的长为200米，则滑雪道的坡顶到坡底垂直高度AB的长为（）

A、200tan20°米 B、 $\frac{200}{sin 20^{\circ}}$ 米 C、200sin20°米 D、200cos20°米

查看试题解析
8. 如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tan∠DCB的值是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
9. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（）

A、 $\frac{1}{1 - sin α}$ B、 $\frac{1}{1 +sin α}$ C、 $\frac{1}{1 - cos α}$ D、 $\frac{1}{1 +cos α}$

查看试题解析
10. 如图，飞机在空中B处探测到它的正下方地面上目标C，此时飞行高度BC=1200米，从飞机上看地面指挥台A的俯角α的正切值为 $\frac{3}{4}$ 则飞机与指挥台之间AB的距离为（）米

A、1200 B、1600 C、1800 D、2000

查看试题解析

二、填空题

11. 如图，△ABC的顶点都是正方形网格中的格点，则tan∠ABC=.

查看试题解析
12. 如图，在平行四边形ABCD中，AE⊥BC，垂足为E，如果AB=5，BC=8， $sin B = \frac{4}{5}$ ，那么EC=.

查看试题解析
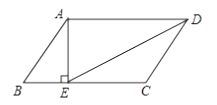13. 计算：tan60°﹣cos30°= ．

查看试题解析
14. 在Rt△ABC中，∠C=90°，AB=2，BC= $\sqrt{3}$ ，则sin $\frac{A}{2}$ =

查看试题解析
15. 如图，一艘海轮位于灯塔P的北偏东60°方向，距离灯塔为4海里的点A处，如果海轮沿正南方向航行到灯塔的正东位置，海轮航行的距离AB长海里．

查看试题解析
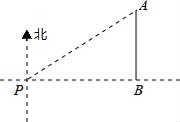16. 4cos30°+ ${(1 - \sqrt{2})}^{0} - \sqrt{12}$ +|﹣2|= ．

查看试题解析
17. 坡角为α=60°，则坡度i= ．

查看试题解析
18. 如图，旗杆高AB=8m，某一时刻，旗杆影子长BC=16m，则tanC=。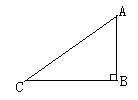

查看试题解析

三、计算题

19. 先化简，再求值：（1﹣ $\frac{a}{a^{2} + a}$ ）÷ $\frac{a^{2} - 1}{a^{2} + 2 a + 1}$ ，其中a=sin30°．

查看试题解析
20. 计算： $\frac{tan 45 °}{cot 30 ° - 2 sin 45 °} - 3 sin 60 ° + 2 cos 45 °$

查看试题解析

四、解答题

21. 如图，在△ABC中，∠A=30°，cosB= $\frac{4}{5}$ ，AC= $6 \sqrt{3}$ .求AB的长.

查看试题解析
22. 汽车超速行驶是交通安全的重大隐患，为了有效降低交通事故的发生，许多道路在事故易发路段设置了区间测速如图，学校附近有一条笔直的公路l，其间设有区间测速，所有车辆限速40千米/小时数学实践活动小组设计了如下活动：在l上确定A，B两点，并在AB路段进行区间测速．在l外取一点P，作PC⊥l，垂足为点C．测得PC=30米，∠APC=71°，∠BPC=35°．上午9时测得一汽车从点A到点B用时6秒，请你用所学的数学知识说明该车是否超速．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin71°≈0.95，cos71°≈0.33，tan71°≈2.90）

查看试题解析
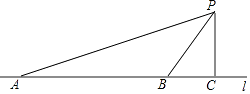23. 如图，一座山的一段斜坡BD的长度为600米，且这段斜坡的坡度i=1：3（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角为33°，在斜坡D处测得山顶A的仰角为45°．求山顶A到地面BC的高度AC是多少米？（结果用含非特殊角的三角函数和根式表示即可）

查看试题解析
24. 如图，A，B两座城市相距100千米，现计划要在两座城市之间修筑一条高等级公路（即线段AB）。经测量，森林保护区中心P点在A城市的北偏东30°方向，B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心，50千米为半径的圆形区域内，请问：计划修筑的这条高等级公路会不会穿越保护区？为什么？

查看试题解析

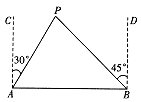
五、综合题

25. 如图，在四边形ABCD中，AD∥BC，∠ABC=90°，AB=AD，连接BD，点E在AB上，且∠BDE=15°，DE=4 $\sqrt{3}$ ，DC=2 $\sqrt{21}$ ．
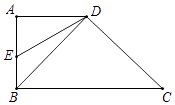
（注意：本题中的计算过程和结果均保留根号）

(1)、求BE的长；

(2)、求四边形DEBC的面积．

查看试题解析
26. 如图1，以▱ABCD的较短边CD为一边作菱形CDEF，使点F落在边AD上，连接BE，交AF于点G.

(1)、猜想BG与EG的数量关系.并说明理由；

(2)、延长DE，BA交于点H，其他条件不变，
①如图2，若∠ADC=60°，求 $\frac{D G}{B H}$ 的值；
②如图3，若∠ADC=α（0°<α<90°），直接写出 $\frac{D G}{B H}$ 的值.（用含α的三角函数表示）

查看试题解析