湘教版九年级上册数学期末测试卷
试卷更新日期:2018-11-19 类型:期末考试
一、单选题
-
1. 下列方程是关于x的一元二次方程的是( )A、ax2+bx+c=0 B、x2+ =0 C、2x+c2=0 D、(x﹣2)(3x+1)=x2. 已知一元二次方程 有一个根为1,则 的值为( )A、-2 B、2 C、-4 D、43. 若点 , , 在反比例函数 的图像上,则 , , 的大小关系是( )A、 B、 C、 D、4. 一元二次方程2x2-x+1=0的根的情况是( )
A、两个不相等的实数根 B、两个相等的实数根 C、没有实数根 D、无法判断5. 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则 = ( ) A、 B、 C、 D、6. 若 , 是函数 图象上的两点,当 时,下列结论正确的是( )
A、 B、 C、 D、6. 若 , 是函数 图象上的两点,当 时,下列结论正确的是( )
A、 B、 C、 D、7. 奉节特产专卖店销售2015年良种夏季脐橙,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克.若该专卖店销售这种脐橙要想平均每天获利2240元,为减少库存,每千克脐橙应降价多少元?( )A、4元 B、6元 C、4元或6元 D、5元8. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )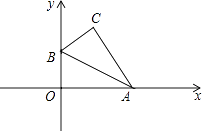 A、 B、 C、 D、9. 如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A、 B、 C、 D、9. 如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( ) A、 B、 C、 D、10. 如图,点A,B在双曲线y= (x>0)上,点C在双曲线y= (x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )
A、 B、 C、 D、10. 如图,点A,B在双曲线y= (x>0)上,点C在双曲线y= (x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )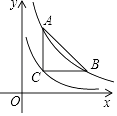 A、 B、2 C、4 D、3
A、 B、2 C、4 D、3二、填空题
-
11. 如果函数 是反比例函数,那么k= .
12. 一元二次方程x2﹣x=0的根是 .13. 已知点C是线段AB的黄金分割点,(AC>BC)若AB=2cm,则AC=cm.14. 若 x1、x2是一元二次方程 的两个实数根,则 = .
15. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .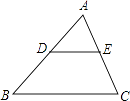 16. 如图,▱ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 .
16. 如图,▱ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 . 17. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=.
17. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=. 18. 如图,矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30°,将△ABE沿BE翻折,得到△A′BE,连接CA′并延长,与AD相交于点F,则DF的长为 .
18. 如图,矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30°,将△ABE沿BE翻折,得到△A′BE,连接CA′并延长,与AD相交于点F,则DF的长为 .
三、计算题
-
19.
(1)、计算: .(2)、解方程: .四、作图题
-
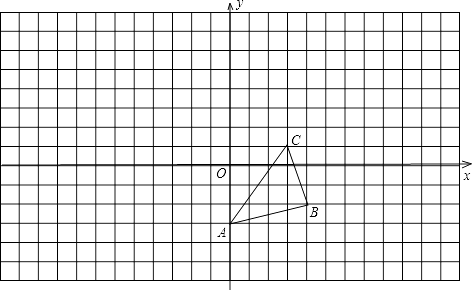
20. 如图,已知O是坐标原点,A、B、C的坐标分别为(0,-3)、(4,-2)、(3,1),以O为位似中心作△ABC的位似三角形(只作一个图形即可),要求:新图与原图的相似比为2,并写出点B和点C的对应点的坐标.
五、解答题
-
21. 运动对学生的成长有着深远的影响,某中学为了解学生每天运动的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间/时
频数/人数
频率
A
0≤t≤0.5
8
0.16
B
0.5≤t≤1
a
0.3
C
1≤t≤1.5
16
0.32
D
1.5≤t≤2
7
b
E
2≤t≤2.5
4
0.08
合计
1
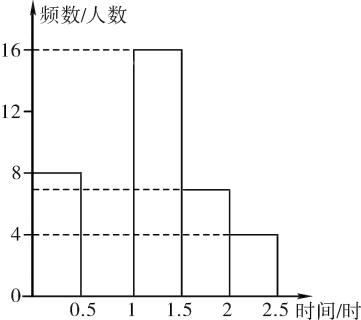
请根据图表中的信息,解答下列问题:
(1)、表中的a= , b= , 中位数落在组,并将频数分布直方图补全;(2)、估计该校3000名学生中,每天运动时间不足0.5小时的学生大约有多少名?(3)、已知E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作运动心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.22. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD). (1)、若所用铁栅栏的长为40米,用含x的代数式表示矩形的长AB;(2)、在(1)的条件下,若使矩形场地面积为192平方米,则AD、AB的长应分别为多少米?23. 如图,平行四边形ABCD中,点E在BA的延长线上,连接CE与AD相交于点F,若BC=8,CD=3,AE=1.求:AF的长.
(1)、若所用铁栅栏的长为40米,用含x的代数式表示矩形的长AB;(2)、在(1)的条件下,若使矩形场地面积为192平方米,则AD、AB的长应分别为多少米?23. 如图,平行四边形ABCD中,点E在BA的延长线上,连接CE与AD相交于点F,若BC=8,CD=3,AE=1.求:AF的长.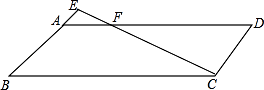 24.
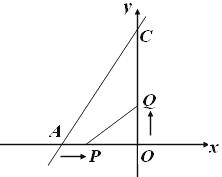
24.如图,已知,在直角坐标系xOy中,直线 y=x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向右移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发,经过几秒钟,能使△PQO的面积为8个平方单位.com
 25. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时)
25. 如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据: , , 结果精确到0.1小时)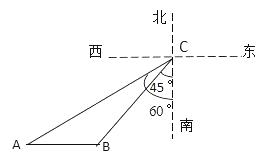
六、综合题
-
26. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ +b=0的一元二次方程称为“勾系一元二次方程”.
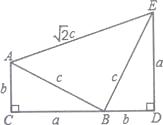
请解决下列问题:
(1)、写出一个“勾系一元二次方程”;
(2)、求证:关于x的“勾系一元二次方程”ax2+ +b=0必有实数根;
(3)、若x=-1是“勾系一元二次方程”ax2+ +b=0的一个根,且四边形ACDE的周长是6 ,求△ABC面积.
-
-