浙教版八年级下册第5章 5.1矩形 同步练习

试卷更新日期：2017-03-22 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 矩形具有而菱形不具有的性质是（  ）
    A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等

    查看试题解析

  • 2. 若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定满足（   ）
    A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线相等且相互平分

    查看试题解析

  • 3. 在一组对边平行的四边形中，增加下列条件中的哪一个条件，这个四边形是矩形（   ）
    A、另一组对边相等，对角线相等 B、另一组对边相等，对角线互相垂直 C、另一组对边平行，对角线相等 D、另一组对边平行，对角线互相垂直

    查看试题解析

  • 4. 若矩形的一条对角线与一边的夹角是40°，则两条对角线所夹的锐角的度数为（   ）
    A、80° B、60° C、45° D、40°

    查看试题解析

  • 5.

    如图，在矩形纸片ABCD中，已知AD=8，折叠纸片，使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为（   ）

    A、3 B、4 C、5 D、6

    查看试题解析

  • 6. 在平面中，下列说法正确的是（   ）
    A、四边相等的四边形是正方形 B、四个角相等的四边形是矩形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形

    查看试题解析

  • 7.

    如图，矩形纸片ABCD中，点E是AD的中点，且AE=1，BE的垂直平分线MN恰好过点C．则矩形的一边AB的长度为（　　）

    A、1 B、2 C、3 D、2

    查看试题解析

  • 8. 如图，把矩形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么下列说法错误的是（   ）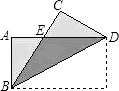

    A、△EBD是等腰三角形，EB=ED B、折叠后∠ABE和∠CBD一定相等 C、折叠后得到的图形是轴对称图形 D、△EBA和△EDC一定是全等三角形

    查看试题解析

  • 9. 如图，矩形ABCD中，AB=1，∠AOB=60°，则BC=（   ）

    A、2 B、3 C、2 D、5

    查看试题解析

  • 10. 菱形具有而矩形不具有的性质是（   ）
    A、对角线互相平分 B、四条边都相等 C、对角相等 D、邻角互补

    查看试题解析

  • 11. 如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是（   ）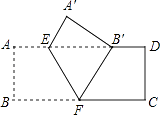

    A、12 B、24 C、12 3 D、16 3

    查看试题解析

  • 12. 如图，小贤为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架ABCD ， B与D两点之间用一根橡皮筋拉直固定，然后向右扭动框架，观察所得四边形的变化，下列判断错误的是（　　）

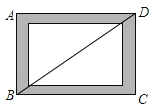    A、四边形ABCD由矩形变为平行四边形 B、BD的长度增大 C、四边形ABCD的面积不变 D、四边形ABCD的周长不变

    查看试题解析

  • 13. 下列命题中，是真命题的是（   ）
    A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形

    查看试题解析

  • 14. 如图所示，点E是矩形ABCD的边AD延长线上的一点，且AD=DE，连结BE交CD于点O，连结AO，下列结论不正确的是（   ）

    A、△AOB≌△BOC B、△BOC≌△EOD C、△AOD≌△EOD D、△AOD≌△BOC

    查看试题解析

  • 15.

    如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形CODE的周长（　　）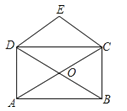

    A、4 B、6 C、8 D、10

    查看试题解析

二、填空题

  • 16. 在矩形ABCD中，对角线AC，BD相交于点O，若∠AOB=80°，则∠OAB的大小为（度）．

    查看试题解析

  • 17. 矩形两条对角线的夹角为60°，其中矩形中较短的边长为5，则矩形对角线的长为 ．

    查看试题解析

  • 18. 如图，△ABC中，∠C=90°，AC=3，AB=5，D为AB边上一点，DE∥AC，交BC于点E，DF∥BC，交AC于点F，连接EF，则线段EF的最小值为

    查看试题解析

  • 19.

    如图，在矩形ABCD中，对角线AC、BD交于点O，若∠AOD=120°，AB=1，则△OAB的周长为 ．

    查看试题解析

  • 20. 如图，在矩形ABCD中，已知∠DBC=45°，∠DBC的平分线交DC于点E，作EF⊥BD于点F，作FG⊥BC于点G，则 BGGC = ．

    查看试题解析

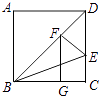
三、解答题

  • 21. 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于N，连接MN，DN．请你判定四边形BMDN是什么特殊四边形，并说明理由．

    查看试题解析

  • 22. 如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=4，设AB=x，AD=y，求x2+（y﹣4）2的值．

    查看试题解析

  • 23. 如图，四边形ABCD是平行四边形，对角线AC，BD相交于点O，且∠1=∠2．求证：四边形ABCD是矩形．

    查看试题解析

四、综合题

  • 24. 已知：菱形ABCD的两条对角线AC，BD交于点O，BE∥AC，CE∥BD．

    (1)、若AC=8，BD=6，求AB的长；
    (2)、求证：四边形OBEC为矩形．

    查看试题解析

  • 25. 如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．

    (1)、求证：AE=DC；
    (2)、已知DC= 2 ，求BE的长．

    查看试题解析

  • 26.

    如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED交线段AB于点G，ED的延长线交线段OA于点H，连CH、CG．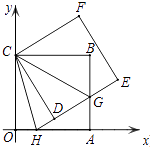

    (1)、求证：△CBG≌△CDG；

    (2)、求∠HCG的度数；并判断线段HG、OH、BG之间的数量关系，说明理由；

    (3)、连结BD、DA、AE、EB得到四边形AEBD，在旋转过程中，当G点在何位置时四边形AEBD是矩形？请说明理由并求出点H的坐标．

    查看试题解析