湖南省邵阳市邵东县2018—2019学年上学期九年级数学期末模拟测试A卷
试卷更新日期:2018-11-19 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )
A、 B、 C、 D、若 ,则x=12. 一元二次方程2x2-x+1=0的根的情况是( )
A、两个不相等的实数根 B、两个相等的实数根 C、没有实数根 D、无法判断3. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人4. 计算:( )﹣1+tan30°•sin60°=( )A、﹣ B、2 C、 D、5. 反比例函数 的图象经过点(-2,3),则该反比例函数图象在( )
A、第一、三象限 B、第二、四象限 C、第二、三象限 D、第一、二象限6. 已知 ,下列变形错误的是( )
A、 B、 C、 D、7. 在同一直角坐标系中,函数y= 和y=kx﹣3的图象大致是( )A、 B、
B、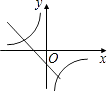 C、
C、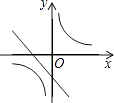 D、
D、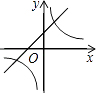 8. 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则 = ( )
8. 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则 = ( ) A、 B、 C、 D、9. 如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )
A、 B、 C、 D、9. 如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )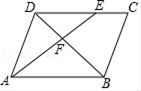 A、2:5 B、3:5 C、9:25 D、4:2510. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A、2:5 B、3:5 C、9:25 D、4:2510. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )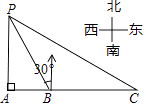 A、40海里 B、60海里 C、20 海里 D、40 海里
A、40海里 B、60海里 C、20 海里 D、40 海里二、填空题
-
11. 一元二次方程x2﹣x=0的根是 .12. 已知关于 的一元二次方程 有两个相等的实数根,则 .13. 已知方程 的两根分别是 、 ,则 , .14. 在△ABC中,∠C=90°,若tanA= ,则sinB= .15. 已知△ABC中,AB=10,AC=2 ,∠B=30°,则△ABC的面积等于 .16. 如图。在 的正方形方格图形中,小正方形的顶点称为格点. 的顶点都在格点上,则 的正弦值是 .
 17. 如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是 .
17. 如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是 .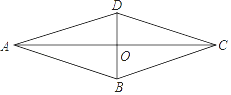 18. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是m(结果保留根号)
18. 如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知甲楼的高AB是120m,则乙楼的高CD是m(结果保留根号)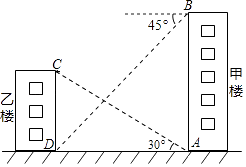
三、计算题
-
19. 解方程:2(x﹣3)=3x(x﹣3).20. 先化简,再求值:( ﹣ )÷ ,其中a=2sin60°﹣tan45°.
四、解答题
-
21. 据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据: ≈1.41, ≈1.73)
 22. 如图,在△ABC中,AB=AC,AD为BC边上的中线DE⊥AB于点E。
22. 如图,在△ABC中,AB=AC,AD为BC边上的中线DE⊥AB于点E。 (1)、求证:△BDE∽△CAD。(2)、若AB=13,BC=10,求线段DE的长23. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表.
(1)、求证:△BDE∽△CAD。(2)、若AB=13,BC=10,求线段DE的长23. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表.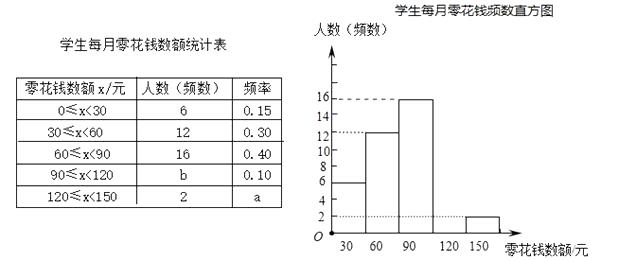
请根据以上图表,解答下列问题:
(1)、这次被调查的人数共有人,a=;
(2)、计算并补全频数分布直方图;
(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数.
24. 如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN. (1)、求证:Rt△ABM≌Rt△AND(2)、线段MN与线段AD相交于T,若AT= ,求 的值
(1)、求证:Rt△ABM≌Rt△AND(2)、线段MN与线段AD相交于T,若AT= ,求 的值五、综合题
-
25. 如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2= (k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC= ,B(m,﹣2)
 (1)、求一次函数和反比例函数的解析式.(2)、结合图象直接写出:当y1>y2时,x的取值范围.26. 如图,在矩形ABCD中,AB=18cm,AD=9cm,点M沿AB边从A点开始向B以2cm/s的速度移动,点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求:
(1)、求一次函数和反比例函数的解析式.(2)、结合图象直接写出:当y1>y2时,x的取值范围.26. 如图,在矩形ABCD中,AB=18cm,AD=9cm,点M沿AB边从A点开始向B以2cm/s的速度移动,点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求: (1)、当t为何值时,∠ANM=45°?
(1)、当t为何值时,∠ANM=45°?
(2)、计算四边形AMCN的面积,根据计算结果提出一个你认为合理的结论;
(3)、当t为何值时,以点M、N、A为顶点的三角形与△BCD相似?