2018-2019学年数学华师大版九年级上册23.3.2 相似三角形的判定(4) 同步练习
试卷更新日期:2018-11-19 类型:同步测试
一、选择题
-
1. 以下条件不可以判定 与 相似的是( )
A、 B、 ,且 C、 , D、 ,且2. 如图,在 的正方形网格中有一只可爱的小狐狸,算算看画面中由实线组成的相似三角形有( )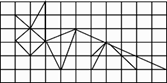 A、4对 B、3对 C、2对 D、1对3. 如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与
A、4对 B、3对 C、2对 D、1对3. 如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 具备下列各组条件的两个三角形中,不一定相似的是( ).
4. 具备下列各组条件的两个三角形中,不一定相似的是( ).
A、有一个角是40°的两个等腰三角形; B、两个等腰直角三角形; C、有一个角为100°的两个等腰三角形; D、两个等边三角形5. 如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( ) A、1对 B、2对 C、3对 D、4对6. △ABC与△DEF满足下列条件,其中能使△ABC∽△DEF的是( )
A、1对 B、2对 C、3对 D、4对6. △ABC与△DEF满足下列条件,其中能使△ABC∽△DEF的是( )
A、AB=1,BC=1.5,AC=2,DE=8,EF=12,DF=16 B、AB= ,BC= ,AC= ,DE= ,EF=3,DF=3 C、AB=3,BC=4,AC=6,DE=6,EF=8,DF=16 D、AB=3,BC=4,AC=5,DE= ,EF=2,DF=7. 将一个直角三角形三边扩大3倍,得到的三角形一定是( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上三种情况都有可能8. 下列所给四对三角形中,根据条件不能判断△ABC与△DEF相似的是 ( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. △ABC的三边长分别为2, , ,△A1B1C1的两边长分别为1和 ,当△A1B1C1的第三边长为时,△ABC∽△A1B1C1.
10. 如图,在大小为 的正方形网格中,是相似三角形的是(请填上编号). 11. 如图,在 中, ,AC=8,BC=6,D是边AB的中点,现有一点P位于边AC上,使得 与 相似,则线段AP的长为 .
11. 如图,在 中, ,AC=8,BC=6,D是边AB的中点,现有一点P位于边AC上,使得 与 相似,则线段AP的长为 . 12. △ABC的三边长分别为 , ,2,△A1B1C1的两边长为1, ,要使△ABC∽△A1B1C1 , 那么△A1B1C1的第三边长为 .
12. △ABC的三边长分别为 , ,2,△A1B1C1的两边长为1, ,要使△ABC∽△A1B1C1 , 那么△A1B1C1的第三边长为 .
13. 一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有种.
14. 如图,△ABC中,AE交BC于点D,∠CAE=∠CBE,AD:DE=3:5,AE=16,BD=8,则DC的长等于 . 15. 如图,等腰直角三角形
15. 如图,等腰直角三角形 中,
中,  =4 cm.点
=4 cm.点  是
是  边上的动点,以
边上的动点,以  为直角边作等腰直角三角形
为直角边作等腰直角三角形  .在点
.在点  从点
从点  移动至点
移动至点  的过程中,点
的过程中,点  移动的路线长为cm.
移动的路线长为cm. 16. 如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC= ,AD=2.当AB=时,△ABC与△ACD相似.
16. 如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC= ,AD=2.当AB=时,△ABC与△ACD相似.
三、解答题
-
17. 已知,在△ABC中,三条边的长分别为2,3,4,△A′B′C′的两边长分别为1,1.5,要使△ABC∽△
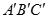 ,求△
,求△ 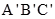 中的第三边长.
中的第三边长.
18. 已知:如图,在△ABC中,点D、E、F分别在AC、AB、BC边上,且四边形CDEF是正方形,AC=3,BC=2,求△ADE、△EFB、△ACB的周长之比和面积之比. 19. 如图,在正方形网格上有 ,这两个三角形相似吗?如果相似,求出 和 的面积比.
19. 如图,在正方形网格上有 ,这两个三角形相似吗?如果相似,求出 和 的面积比. 20. 已知:如图,∠1=∠2,AB•AC=AD•AE.求证:∠C=∠E.
20. 已知:如图,∠1=∠2,AB•AC=AD•AE.求证:∠C=∠E. 21. 已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
21. 已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长. 22. 如图,在正方形ABCD中,E,F分别是边AD,CD上的点, 并延长交BC的延长线于点G
22. 如图,在正方形ABCD中,E,F分别是边AD,CD上的点, 并延长交BC的延长线于点G (1)、求证: ;(2)、若正方形的边长为4,求BG的长.23. 如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1 , P2 , P3 , P4 , P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)、求证: ;(2)、若正方形的边长为4,求BG的长.23. 如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1 , P2 , P3 , P4 , P5是△DEF边上的5个格点,请按要求完成下列各题: (1)、试证明三角形△ABC为直角三角形;
(1)、试证明三角形△ABC为直角三角形;
(2)、判断△ABC和△DEF是否相似,并说明理由;(3)、画一个三角形,使它的三个顶点为P1 , P2 , P3 , P4 , P5中的3个格点并且与△ABC相似(要求:不写作法与证明).