广东省佛山市2018-2019年上学期八年级数学期中测试卷
试卷更新日期:2018-11-18 类型:期中考试
一、单选题
-
1. 4的算术平方根为( )
A、2 B、-2 C、±2 D、162. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间3. 已知三组数据:①3,7,9;②5,12,13;③1, ,2;④7,24,25.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有( )A、1个 B、2个 C、3个 D、4个4. 如图,数轴上A,B两点分别对应实数a、b,则下列结论中正确的是( ) A、a+b>0 B、ab>0 C、 D、a+ab-b<05. 如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A、a+b>0 B、ab>0 C、 D、a+ab-b<05. 如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )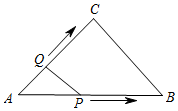 A、
A、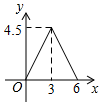 B、
B、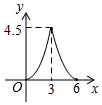 C、
C、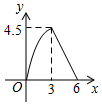 D、
D、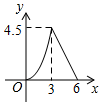 6. 已知点A在x轴的上方,在y轴的左侧,且距离x轴3个单位,且距离y轴4个单位,那么A点的坐标是( )
6. 已知点A在x轴的上方,在y轴的左侧,且距离x轴3个单位,且距离y轴4个单位,那么A点的坐标是( )
A、(-4,3) B、(4,-3) C、(-3,4) D、( -4, -3)7. 对于一次函数y=-2x+4,下列结论错误的是( )
A、函数值随自变量的增大而减小 B、函数的图象不经过第三象限 C、函数的图象向下平移 4 个单位长度得y=-2x 的图象 D、函数的图象与x轴的交点坐标是(0,4)8. 已知 ,则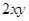 的值为( ) A、
的值为( ) A、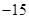 B、
B、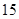 C、
C、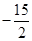 D、
9. 如图,方格纸上一圆直径经过(2,5)、(2,-3)两点,则该圆圆心的坐标为( )
D、
9. 如图,方格纸上一圆直径经过(2,5)、(2,-3)两点,则该圆圆心的坐标为( )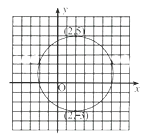 A、(2,-1) B、(2,2) C、(2,1) D、(3,1)10. 一位无线电爱好者把天线杆设在接收效果最佳的矩形屋顶之上.然后,他从杆顶到屋顶四角之间安装固定用的支撑线.有两根相对的支撑线分别长7米和4米,另一根长1米,则最后一根的长度应为( )
A、(2,-1) B、(2,2) C、(2,1) D、(3,1)10. 一位无线电爱好者把天线杆设在接收效果最佳的矩形屋顶之上.然后,他从杆顶到屋顶四角之间安装固定用的支撑线.有两根相对的支撑线分别长7米和4米,另一根长1米,则最后一根的长度应为( )
A、8米 B、9米 C、10米 D、12米二、填空题
-
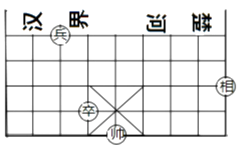
11. 如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为。
 12. 一个正数的平方根分别是x+1和x﹣5,则x= .13. 观察下列运算过程:
12. 一个正数的平方根分别是x+1和x﹣5,则x= .13. 观察下列运算过程:……
请运用上面的运算方法计算:
= .
14. 若三角形的三边长分别等于 , ,2,则此三角形的面积为 .
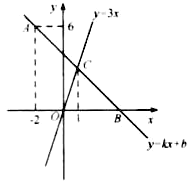
15. 如图,将直线OA向上平移1个单位,得到一个一次函数的图象,那么这个一次函数的解析式是 .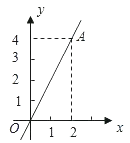 16. 已知点A(x1 , y1)、B(x2 , y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为.
16. 已知点A(x1 , y1)、B(x2 , y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为.三、计算题
-
17. 计算: .18. 计算﹣(﹣2)+(π﹣3.14)0+ +(﹣ )﹣1
四、解答题
-
19. 在平面直角坐标系中,一次函数y=kx+2的图象经过点(2,1).
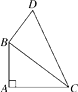
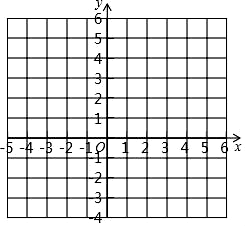 (1)、求k的值,并画出该函数的图象;(2)、若y=kx+2的图象与y=x+5的图象相交于点P,试判断P点的象限并说明理由.20. 如图所示,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.
(1)、求k的值,并画出该函数的图象;(2)、若y=kx+2的图象与y=x+5的图象相交于点P,试判断P点的象限并说明理由.20. 如图所示,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.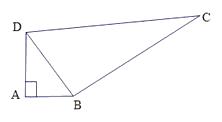 21.
21.某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
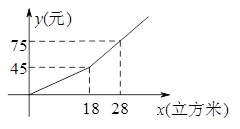 (1)、若某月用水量为18立方米,则应交水费多少元?(2)、求当x>18时,y关于x的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?22. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
(1)、若某月用水量为18立方米,则应交水费多少元?(2)、求当x>18时,y关于x的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?22. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:若日销售量y是销售价x的一次函数.
x (元)
15
20
25
…
y (件)
25
20
15
…
(1)、求出日销售量y(件)与销售价x(元)的函数关系式;
(2)、求销售价定为30元时,每日的销售利润.