湘教版九年级上学期数学期末考试试卷
试卷更新日期:2018-11-18 类型:期末考试
一、单选题
-
1. 下列函数是反比例函数的是( )
A、 B、y= C、y=x²+2x D、y=4x+82. 已知点 、 都在反比例函数 的图象上,则下列关系式一定正确的是( )A、 B、 C、 D、3. 关于x的一元二次方程x2﹣3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、m< B、m≤ C、m> D、m≥4. 共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A、1000(1+x)2=1000+440 B、1000(1+x)2=440 C、440(1+x)2=1000 D、1000(1+2x)=1000+4405. 在同一直角坐标系中,函数y= 和y=kx﹣3的图象大致是( )A、 B、
B、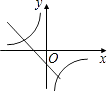 C、
C、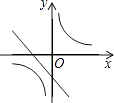 D、
D、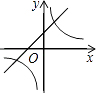 6. 如图,下列条件中不能判定△ACD∽△ABC的是( )
6. 如图,下列条件中不能判定△ACD∽△ABC的是( )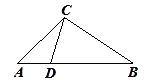 A、 B、∠ADC=∠ACB C、∠ACD=∠B D、AC2=AD·AB7. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )A、3 B、 C、 D、8. 体育老师对甲、乙两名同学分别进行了8次摸高测试,这两名同学成绩的平均数不相等,甲同学的方差是S =6.4,乙同学的方差是S =8.2,那么这两名同学摸高成绩比较稳定的是( )
A、 B、∠ADC=∠ACB C、∠ACD=∠B D、AC2=AD·AB7. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )A、3 B、 C、 D、8. 体育老师对甲、乙两名同学分别进行了8次摸高测试,这两名同学成绩的平均数不相等,甲同学的方差是S =6.4,乙同学的方差是S =8.2,那么这两名同学摸高成绩比较稳定的是( )
A、甲 B、乙 C、甲乙一样 D、无法确定9. 函数y1=x和y2= 的图象如图所示,则y1>y2的x取值范围是( )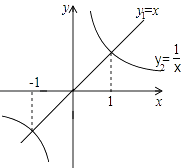 A、x<﹣1或x>1 B、x<﹣1或0<x<1 C、﹣1<x<0或x>1 D、﹣1<x<0或0<x<110. 一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )
A、x<﹣1或x>1 B、x<﹣1或0<x<1 C、﹣1<x<0或x>1 D、﹣1<x<0或0<x<110. 一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm,现沿底边从下到上依次裁剪宽度均为3cm的矩形纸条(如图所示),则裁得的纸条中恰为张正方形的纸条是( )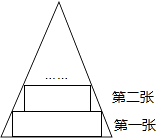 A、第4张 B、第5张 C、第6张 D、第7张
A、第4张 B、第5张 C、第6张 D、第7张二、填空题
-
11. 已知 = ,则 的值为 .12. 方程 是一元二次方程,则m= .
13. 已知|sinA﹣ |+ =0,那么∠A+∠B= .
14. 设 、 是一元二次方程 的两个根,且 ,则 , .15. 如图。在 的正方形方格图形中,小正方形的顶点称为格点. 的顶点都在格点上,则 的正弦值是 . 16. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
16. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .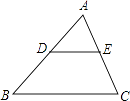 17.
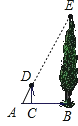
17.如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为m.
 18. 如图,在矩形 中, , ,将矩形 沿 折叠,点 落在 处,若 的延长线恰好过点 ,则 的值为 .
18. 如图,在矩形 中, , ,将矩形 沿 折叠,点 落在 处,若 的延长线恰好过点 ,则 的值为 .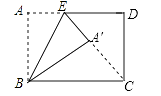
三、计算题
-
19. 解方程:
(1)、x2-2x-8=0;(2)、(x-2)(x-5)=-2.四、作图题
-
20. 如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).

①画出△ABC关于x轴对称的△A1B1C1;
②以原点O为位似中心,在x轴的上方画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
五、综合题
-
21. 某地2015年为做好“精准扶贫”,投入资金 1280 万元用于异地安置,并规划投入资金逐年增加, 2017 年在 2015 年的基础上增加投入资金 1600 万元.(1)、从 2015 年到 2017 年,该地投入异地安置资金的年平均增长率为多少?(2)、在 2017 年异地安置的具体实施中,该地计划投入资金不低于 500 万元用于优先搬迁租房奖励,规定前 1000 户(含第 1000 户)每户每天奖励8元, 1000 户以后每户每天奖励5元,按租房 400 天计算,求 2017 年该地至少有多少户享受到优先搬迁租房奖励.
22. 直线y=kx+b与反比例函数y= (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.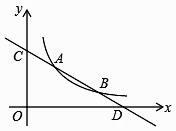 (1)、求直线AB的解析式;(2)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.23. 某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部分为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):
(1)、求直线AB的解析式;(2)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.23. 某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部分为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):抽取的男生“引体向上”成绩统计表
成绩
人数
0分
32
1分
30
2分
24
3分
11
4分
15
5分及以上
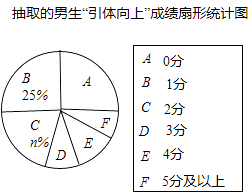
请你根据统计图表中的信息,解答下列问题:
(1)、 填空: , ;(2)、 求扇形统计图中 组的扇形圆心角的度数;(3)、目前该市八年级有男生3600名,请估计其中“引体向上”得零分的人数.24. 如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.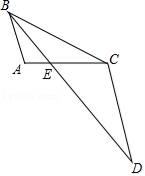 (1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.
(1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.
25. 小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问: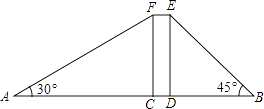 (1)、楼高多少米?(2)、若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: ≈1.73, ≈1.41, ≈2.24)
(1)、楼高多少米?(2)、若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: ≈1.73, ≈1.41, ≈2.24)
26. 如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD//BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).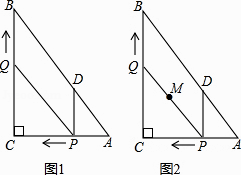 (1)、直接用含t的代数式分别表示:QB= , PD= .(2)、是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)、如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
(1)、直接用含t的代数式分别表示:QB= , PD= .(2)、是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)、如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
-
-