江苏省兴化市顾庄学区三校2016-2017学年七年级下学期第一次月考数学试卷
试卷更新日期:2017-03-22 类型:月考试卷
一、选择题
-
1. 等于( )
A、 B、 C、 D、2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.00 000 0076克,用科学记数法表示是A、7.6×108克 B、7.6×10-7克 C、7.6×10-8克 D、7.6×10-9克3. 在下列多项式乘法运算中,不能运用平方差公式进行运算的是( )A、(2x+3y) (-2x+3y) B、(a-2b) (a+2b) C、(-x-2y) (x+2y) D、(-2x-3y) (3y -2x)4. 如图1,在边长为 a 的正方形中挖掉一个边长为 b 的小正方形 ,把余下的部分剪拼成一长方形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )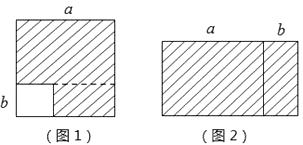 A、 B、 C、 D、5. 下列长度的三根木棒首尾相接,不能做成三角形框架的是( )A、5cm,7cm,10cm B、5cm,7cm,13cm C、7cm,10cm,13cm D、5cm,10cm,13cm6.
A、 B、 C、 D、5. 下列长度的三根木棒首尾相接,不能做成三角形框架的是( )A、5cm,7cm,10cm B、5cm,7cm,13cm C、7cm,10cm,13cm D、5cm,10cm,13cm6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数 等于( )
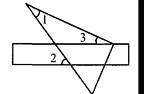 A、20° B、50° C、30° D、15°
A、20° B、50° C、30° D、15°二、填空题
-
7. 计算:x2·x4=.8. 若5x=12,5y=4,则5x-y=.9. 已知 ,则 =.10. 若a-b=1,ab=-2,则(a+1)(b-1)=.11. 如果(x+1)(x+m)的积中不含x的一次项,则m的值为.12. 七边形的内角和是度.13.
在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于度.
 14.
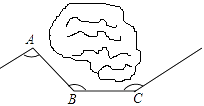
14.如图,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A=130°,第二次拐角∠B=150° . 第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C为度.
 15.
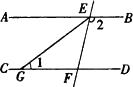
15.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=35º,那么∠2=度.
 16. 已知 , 则 =.
16. 已知 , 则 =.三、解答题
-
17. 计算:①
②a2·a4+(a2)3
18. 计算:①②
③
④
19. 先化简,再求值: ,其中a=﹣3,b= .20. 一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.21. 已知a , b为常数,且三个单项式4xy2 , axyb , -5xy相加得到的和仍然是单项式。那么a和b的值可能是多少?说明你的理由。22. ①已知am=2,an=3,求am+2n的值。②已知 ,求xy的值。
23.如图,BD是∠ABC的角平分线,DE∥BC,交AB于点E,∠A=45°, ∠BDC=60°。
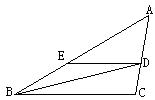 (1)、求∠C的度数;(2)、求∠BED的度数.24.
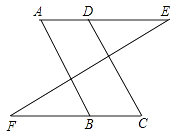
(1)、求∠C的度数;(2)、求∠BED的度数.24.如图,已知∠A = ∠C,∠E=∠F。试说明AB∥CD。
 25. 探究与发现:
25. 探究与发现: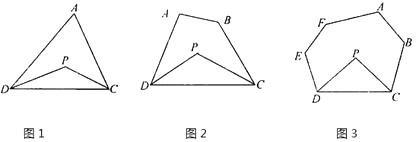 (1)、探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
(1)、探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)、探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)、探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
26. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 如图1,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2.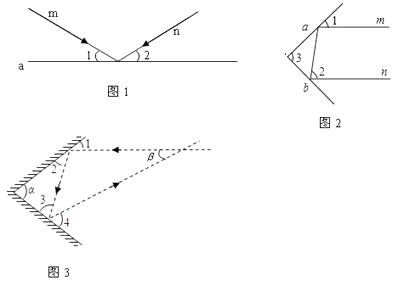 (1)、如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=°,∠3=°.(2)、在(1)中m∥n,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°.(3)、由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?(4)、如图3,两面镜子的夹角为α°(0<α<90)时,进入光线与离开光线的夹角为β°
(1)、如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=°,∠3=°.(2)、在(1)中m∥n,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°.(3)、由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?(4)、如图3,两面镜子的夹角为α°(0<α<90)时,进入光线与离开光线的夹角为β°(0<β<90).试探索α与β的数量关系.直接写出答案.