江西省吉安市吉州区2018-2019学年上学期八年级数学期末模拟测试卷
试卷更新日期:2018-11-17 类型:期末考试
一、单选题
-
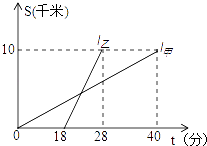
1. 在△ABC中,∠A=90°,∠A,∠B,∠C的对边长分别为a、b、c,则下列结论错误的是( )A、a2+b2=c2 B、b2+c2=a2 C、a2-b2=c2 D、a2-c2=b22. π、 ,﹣ , ,3.1416,0. 中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个3. 已知点A在x轴上,且点A到y轴的距离为4,则点A的坐标为( )A、(4,0) B、(0,4) C、(4,0)或(-4,0) D、(0,4)或(0,-4)4. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
 A、4个 B、3个 C、2个 D、1个5. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )
A、4个 B、3个 C、2个 D、1个5. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )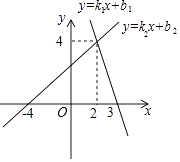 A、 B、 C、 D、6. 如图,在△ABC中,∠A=60°,∠ABC=50°,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是( )
A、 B、 C、 D、6. 如图,在△ABC中,∠A=60°,∠ABC=50°,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是( )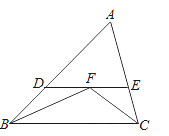
①∠ACB=70°;②∠BFC=115°;③∠BDF=130°;④∠CFE=40°.
A、①② B、③④ C、①③ D、①②③二、填空题
-
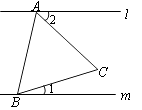
7. 一组数据2,3,3,1,5的众数是 .8. 如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=.
 9. 已知x,y都是实数,且y= + +4,则yx=.10. 如图,已知函数y=x﹣2和y=﹣2x+1的图象交于点P(1,﹣1),根据图象可得方程组 的解是 .
9. 已知x,y都是实数,且y= + +4,则yx=.10. 如图,已知函数y=x﹣2和y=﹣2x+1的图象交于点P(1,﹣1),根据图象可得方程组 的解是 .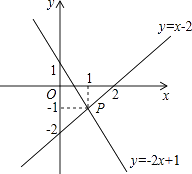 11. 已知:点A(m,2)与点B(3,n)关于y轴对称,则(m+n)2016= .12. 在平面直角坐标系xOy中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y=kx+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形,如果A1(1,1),A2( ),那么点An的纵坐标是 .
11. 已知:点A(m,2)与点B(3,n)关于y轴对称,则(m+n)2016= .12. 在平面直角坐标系xOy中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y=kx+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形,如果A1(1,1),A2( ),那么点An的纵坐标是 .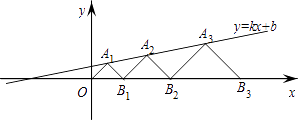
三、计算题
-
13. 求值:(﹣1)2018+|1﹣ |﹣14. 解方程组:
四、解答题
-
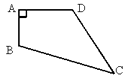
15. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积.
 16. 已知y-1与2x+3是正比例关系, y是关于x的一次函数吗?请说明理由.17. 小明和小华同时解方程组 ,小明看错了m , 解得 ,小华看错了n , 解得 ,你能知道原方程组正确的解吗?18. 如图,在△ABC 和△DEF 中,点 B、F、C、E 在同一直线上,BF=CE,AC∥DF 且 AC=DF. 求证:AB∥DE.
16. 已知y-1与2x+3是正比例关系, y是关于x的一次函数吗?请说明理由.17. 小明和小华同时解方程组 ,小明看错了m , 解得 ,小华看错了n , 解得 ,你能知道原方程组正确的解吗?18. 如图,在△ABC 和△DEF 中,点 B、F、C、E 在同一直线上,BF=CE,AC∥DF 且 AC=DF. 求证:AB∥DE.
五、作图题
-
19. 正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,
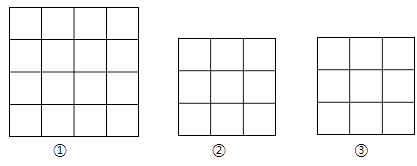 (1)、在图①中,画一个面积为10的正方形;
(1)、在图①中,画一个面积为10的正方形;
(2)、在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都不是整数.
六、综合题
-
20. 某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)、甲乙两种材料每千克分别是多少元?
(2)、现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)、在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
21. 阅读理解∵ < < ,即2< <3.
∴ 的整数部分为2,小数部分为 ﹣2,
∴1< ﹣1<2
∴ ﹣1的整数部分为1.
∴ ﹣1的小数部分为 ﹣2
解决问题:已知:a是 ﹣3的整数部分,b是 ﹣3的小数部分,
求:
(1)、a,b的值;(2)、(﹣a)3+(b+4)2的平方根.
22. 我市某中学举行“中国梦•校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.(方差公式:s2= [(x1﹣ )2+(x2﹣ )2+…+(xn﹣ )2])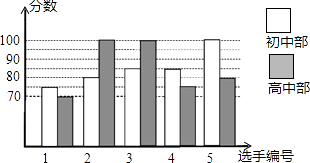 (1)、根据图示填写表格单位(分);
(1)、根据图示填写表格单位(分);平均数/分
中位数/分
众数/分
初中代表队
85
高中代表队
85
100
(2)、结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好?(3)、计算两队决赛成绩的方差判断哪一个代表队选手成绩较为稳定.23. 如图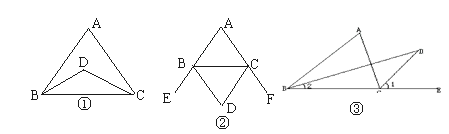 (1)、如图①,BD、CD是∠ABC和∠ACB的角平分线且相交于点D,请猜想∠A与∠BDC之间的数量关系,并说明理由。(2)、如图②,BC、CD是∠ABC和∠ACB外角的平分线且相交于点D。(3)、如图③,BD为∠ABC的角平分线,CD为∠ABC的外角的角平分线,它们相交于点D,猜想∠A与∠D之间的数量关系,并说明理由。24. 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)、如图①,BD、CD是∠ABC和∠ACB的角平分线且相交于点D,请猜想∠A与∠BDC之间的数量关系,并说明理由。(2)、如图②,BC、CD是∠ABC和∠ACB外角的平分线且相交于点D。(3)、如图③,BD为∠ABC的角平分线,CD为∠ABC的外角的角平分线,它们相交于点D,猜想∠A与∠D之间的数量关系,并说明理由。24. 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).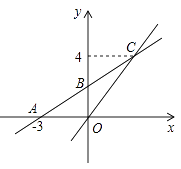 (1)、求正比例函数与一次函数的关系式;(2)、若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;(3)、在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(1)、求正比例函数与一次函数的关系式;(2)、若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;(3)、在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)、在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
-