湖北省宜昌市2018-2019学年人教版九年级上学期数学期中测试卷
试卷更新日期:2018-11-17 类型:期中考试
一、单选题
-
1. 下列方程中,一元二次方程是( )A、 =0 B、 C、 D、2. 一元二次方程5x2-1-4x=0的一次项系数是( )
A、-1 B、-4 C、4 D、53. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、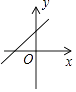 B、
B、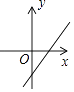 C、
C、 D、
D、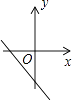 4. 如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
4. 如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )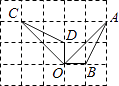 A、30° B、45° C、90° D、135°5. 下列所述图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、菱形 C、平行四边形 D、等腰三角形6. 已知函数y1=x2与函数y2=-x+3的图象大致如图.若y1≤y2则自变量的取值范围是( ).
A、30° B、45° C、90° D、135°5. 下列所述图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、菱形 C、平行四边形 D、等腰三角形6. 已知函数y1=x2与函数y2=-x+3的图象大致如图.若y1≤y2则自变量的取值范围是( ).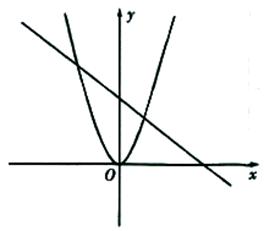
A、-<x<2 B、x>2或x<- C、-2≤x≤ D、x<-2或x>7. 若 、 是一元二次方程 的两个实数根,则 的值为( )A、 B、 C、 D、8. 以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A、b≥ B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤29. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-1,则 的值为( )
A、3或6 B、1或6 C、1或3 D、4或610. 抛物线y=﹣ (x+ )2﹣3的顶点坐标是( )A、( ,﹣3) B、(﹣ ,﹣3) C、( ,3) D、(﹣ ,3)11. 抛物线y=-2x2+1的对称轴是( )A、直线 B、直线 C、y轴 D、直线x=212. 在平面直角坐标系中,点P(﹣20,a)与点Q(b,13)关于原点对称,则a+b的值为( )A、33 B、﹣33 C、﹣7 D、713. 抛物线y=3x2﹣3向右平移3个单位长度,得到新抛物线的表达式为( )A、y=3(x﹣3)2﹣3 B、y=3x2 C、y=3(x+3)2﹣3 D、y=3x2﹣614. 对于二次函数y=−(x−1)2+2的图象与性质,下列说法正确的是( )
A、对称轴是直线x=1,最小值是2 B、对称轴是直线x=1,最大值是2 C、对称轴是直线x=−1,最小值是2 D、对称轴是直线x=−1,最大值是215.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
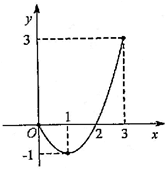 A、有最小值0,有最大值3 B、有最小值﹣1,有最大值0 C、有最小值﹣1,有最大值3 D、有最小值﹣1,无最大值
A、有最小值0,有最大值3 B、有最小值﹣1,有最大值0 C、有最小值﹣1,有最大值3 D、有最小值﹣1,无最大值二、解答题
-
16. 解方程:
(1)x2﹣3x﹣1=0.
(2)x2+4x﹣2=0.
17. 已知关于x的一元二次方程(m﹣2)x2+2mx+m+3=0 有两个不相等的实数根.(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求方程的根.
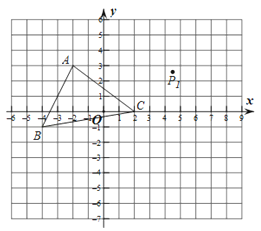
18.在平面直角坐标系中,△ABC的顶点坐标是A(﹣2,3),B(﹣4,﹣1),C(2,0).点P(m,n)为△ABC内一点,平移△ABC得到△A1B1C1 , 使点P(m,n)移到P(m+6,n+1)处.
(1)请直接写出点A1 , B1 , C1的坐标;
(2)将△ABC绕坐标点C逆时针旋转90°得到△A2B2C,画出△A2B2C;
(3)直接写出△ABC的面积.
 19. 设等腰三角形的三条边分别为3、m、n,已知m、n是关于x的方程x2﹣4x+k=0的两个根,求k的值.20.
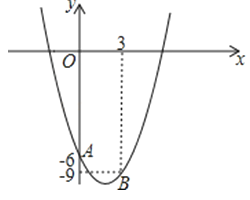
19. 设等腰三角形的三条边分别为3、m、n,已知m、n是关于x的方程x2﹣4x+k=0的两个根,求k的值.20.如图,已知抛物线y=ax2﹣4x+c经过点A(0,﹣6)和B(3,﹣9).
(1)求出抛物线的解析式;
(2)写出抛物线的对称轴方程及顶点坐标;
(3)点P(m,m)与点Q均在抛物线上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q的坐标;
(4)在满足(3)的情况下,在抛物线的对称轴上寻找一点M,使得△QMA的周长最小.
 21. 某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.
21. 某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.(Ⅰ)求y与x的函数关系式,并直接写出自变量x的取值范围;求x为何值时y的值为1920?
(Ⅱ)每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
22.某住宅小区在住宅建设时留下一块1798平方米的空地,准备建一个矩形的露天游泳池,设计如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带
(1)请你计算出游泳池的长和宽;
(2)若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,请你计算要贴瓷砖的总面积.
 23.
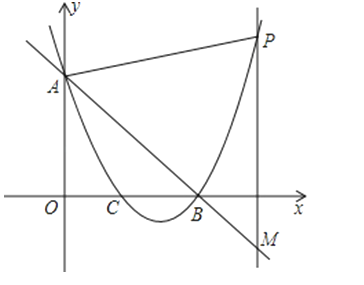
23.如图,已知抛物线y=x2+bx+c与直线y=﹣x+3交于A、B两点,点A 在y轴上,点B在x轴上,抛物线与x轴的另一交点为C,点P在点B右边的抛物线上,PM⊥x轴交直线AB于M.
(1)求抛物线解析式.
(2)当PM=2BC时,求M的坐标.
(3)点P运动过程中,△APM能否为等腰三角形?若能,求点P的坐标,若不能说明理由.
 24.
24.抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
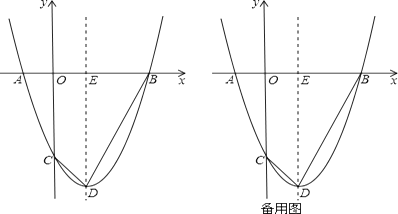 (1)、求点B及点D的坐标.(2)、连结BD,CD,抛物线的对称轴与x轴交于点E.
(1)、求点B及点D的坐标.(2)、连结BD,CD,抛物线的对称轴与x轴交于点E.①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.