浙江省台州市2019届九年级上学期数学期中考试试卷
试卷更新日期:2018-11-16 类型:期中考试
一、选择题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知⊙O的半径为5,若OP=6,则点P与⊙O的位置关系是( )
2. 已知⊙O的半径为5,若OP=6,则点P与⊙O的位置关系是( )
A、点P在⊙O内 B、点P在⊙O外 C、点P在⊙O上 D、无法判断3. 已知一元二次方程x2+kx-3=0有一个根为1,则另一根为( )A、-3 B、-2 C、2 D、34. 如图,A , B , C是⊙O上的三点,∠ABO=25°,∠ACO=30°,则∠BOC的度数为( ) A、100° B、110° C、125° D、130°5. 随着台州市打造“和合圣地”的推进,某企业推出以“和合文化”为载体的产品,2017年盈利50万元,计划到2019年盈利84.5万元,则该产品的年平均增长率为( )
A、100° B、110° C、125° D、130°5. 随着台州市打造“和合圣地”的推进,某企业推出以“和合文化”为载体的产品,2017年盈利50万元,计划到2019年盈利84.5万元,则该产品的年平均增长率为( )
A、20% B、30% C、34.5% D、69%6. 二次函数y=x2-4x+3,当0≤x≤5时,y的取值范围为( )
A、3≤y≤8 B、0≤y≤8 C、1≤y≤3 D、-1≤y≤87. 如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=3,则AE的长为( )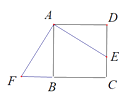 A、 B、5 C、8 D、48. 如图,AB为⊙O的直径,AB=6,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD , 则线段OD的长( )
A、 B、5 C、8 D、48. 如图,AB为⊙O的直径,AB=6,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD , 则线段OD的长( )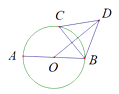 A、随点C的运动而变化,最大值为3 B、随点C的运动而变化,最小值为3 C、随点C的运动而变化,最大值为6 D、随点C的运动而变化,但无最值9. 已知函数y=ax2+2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥-1时,y随x的增大而减小 D、若a<0,则当x≤-1时,y随x的增大而增大10. 如图,在△ABC中,∠B=90°,∠C=30°,AB=6cm , 动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以 cm/s的速度移动,设△BPQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A、随点C的运动而变化,最大值为3 B、随点C的运动而变化,最小值为3 C、随点C的运动而变化,最大值为6 D、随点C的运动而变化,但无最值9. 已知函数y=ax2+2ax﹣1(a是常数,a≠0),下列结论正确的是( )A、当a=1时,函数图象过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a>0,则当x≥-1时,y随x的增大而减小 D、若a<0,则当x≤-1时,y随x的增大而增大10. 如图,在△ABC中,∠B=90°,∠C=30°,AB=6cm , 动点P从点B开始沿边BA、AC向点C以3cm/s的速度移动,动点Q从点B开始沿边BC向点C以 cm/s的速度移动,设△BPQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )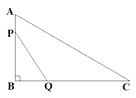 A、
A、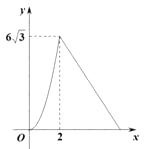 B、
B、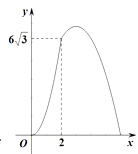 C、
C、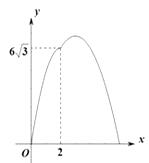 D、
D、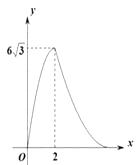
二、填空题
-
11. 已知点A(-1,-2)与点B(m , 2)关于原点对称,则m的值是 .
12. 将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 .
13. 如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针方向旋转得到△A′BC′,点A′恰好落在边AC上,连接CC′,则∠ACC′= .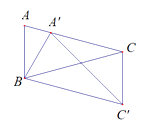 14. 已知关于x的方程 的两根为1和2,则方程 的两根分别 .
14. 已知关于x的方程 的两根为1和2,则方程 的两根分别 .
15. 如图,⊙O是△ABC的外接圆,BC为直径,BC=4,点E是△ABC的内心,连接AE并延长交⊙O于点D,则DE= . 16. 如图,在正方形ABCD中,AB=3,点E , F分别在CD , AD上,CE=DF , BE , CF相交于点G , 连接DG .点E从点C运动到点D的过程中,DG的最小值为 .
16. 如图,在正方形ABCD中,AB=3,点E , F分别在CD , AD上,CE=DF , BE , CF相交于点G , 连接DG .点E从点C运动到点D的过程中,DG的最小值为 .
三、解答题
-
17. 解方程:
(1)、 ;(2)、 .18. 已知,如图,AD=BC.求证:AB=CD
 . 19. 判断关于x的方程(a-2)x2-ax+1=0的根的情况,并说明理由.
. 19. 判断关于x的方程(a-2)x2-ax+1=0的根的情况,并说明理由.
20. 某农户承包荒山种植某产品种蜜柚.已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示. (1)、求y与x的函数关系式,并写出x的取值范围;(2)、当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?21. 如图,在△ABC中,已知∠ABC=120°,AC=4.
(1)、求y与x的函数关系式,并写出x的取值范围;(2)、当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?21. 如图,在△ABC中,已知∠ABC=120°,AC=4. (1)、用直尺和圆规作出△ABC的外接圆⊙O;(不写作法,保留作图痕迹)(2)、求∠AOC的度数;(3)、求 ⊙O的半径.22. 阅读下列材料:求函数 的最大值.
(1)、用直尺和圆规作出△ABC的外接圆⊙O;(不写作法,保留作图痕迹)(2)、求∠AOC的度数;(3)、求 ⊙O的半径.22. 阅读下列材料:求函数 的最大值.解:将原函数转化成关于
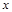 的一元二次方程,得 .
的一元二次方程,得 .当 时,∵x为实数,∴△=
∴ 且 ;
当 时,
 即为 ,方程有解( 的值存在);
即为 ,方程有解( 的值存在);∴ .因此,
 的最大值为4.
的最大值为4.根据材料给你的启示,求函数 的最小值.


