2018-2019学年数学华师大版九年级上册23.3相似三角形（2） 同步练习
试卷更新日期：2018-11-16 类型：同步测试
一、选择题
-
1.
如图，△ABC中，∠C=90°，CD⊥AB，DE⊥AC，则图中与△ABC相似的三角形有（ ）
A、1个 B、2个 C、3个 D、4个2. 在直角三角形ABC中，CD是斜边上的高线，则下列各式能成立的是（ ）
A、 B、 C、 D、3. 如图，在Rt△ABC中，CD是斜边AB上的高，则下列结论正确的是（ ）
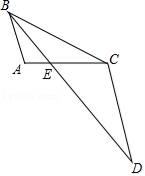
A、BD= AD B、BC2=AB•CD C、AD2=BD•AB D、CD2=AD•BD4. 如图，在Rt△ABC中，∠BAC=90°，AD⊥BC，若AB=2，BC=4．则DC的长度为（ ）
A、1 B、 C、3 D、25. 如图，在△ABC中，∠AED=∠B，则下列等式成立的是 （ ）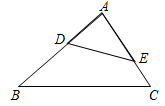
A、 B、 C、 D、6. 如图，菱形ABCD中，点M，N在AC上，NM=AN， ， ；若NF=2，则ME=（ ）
A、2 B、3 C、4 D、57. 如图，等边△ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60°，则CD的长是（ ）
A、 B、 C、 D、8. 如图，在 中，AB=AC=8，∠A＝36°，BD平分 交AC于点D，则 AD=（ ）
A、4 B、4 -4 C、-4 +4 D、4 -4或-4 +4二、填空题
-
9. 如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段 的长为 ．
10. 如图， 中， ， ，垂足为D，若AD=2，BD=4，则CD为 ．
11. 如图，∠BAC＝80°，∠B＝40°，∠E=60°，若将图中的△ADE旋转(平移)，则所得到的新三角形与△ABC ， 与△ADE
12. 如图，点D、E分别在AB、AC上，且∠ABC＝∠AED．若DE＝4，AE＝5，BC＝8，则AB的长为
13. 如图，在△ABC中，AB＝3， AC＝6，将△ABC绕点C按逆时针方向旋转得到△A1B1C使CB1∥AD，分别延长AB，CA1相交于点D，则线段BD的长为 ．
14. 如图，△ABC中，∠AED=∠B，AD=2，DB=4，AE=3，则EC= ．
15. 如图，Rt△ABC中，∠BAC=90°，AB=3，AC=6 ，点D，E分别是边BC，AC上的动点，则DA+DE的最小值为 ．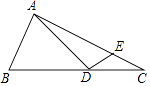
三、解答题
-
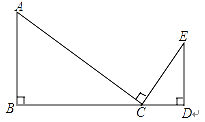
16. 如图，在△ABC和△CDE中，∠B=∠D=90°，C为线段BD上一点，且AC⊥CE，证明：△ABC∽△CDE．
17. 如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F． 求证：△ACD∽△BFD．
18. 如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE．求证：△ABE∽△ACD．
