2018-2019学年数学华师大版九年级上册23.3相似三角形（1） 同步练习
试卷更新日期：2018-11-16 类型：同步测试
一、选择题
-
1. 如图，矩形ABCD中，AE=BF，EF与BD相交于点G，则图中相似三角形共有（ ）
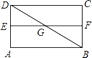A、2对 B、4对 C、6对 D、8对2. 如图，在 中， ，DE分别与AB，AC相交于点D，E，若EC=1，AC=3，则DE：BC的值为（ ）
A、 B、 C、 D、3. 如图，小伟在打网球时，击球点距离球网的水平距离是8米．已知网高是0.8米，要使球恰好能打过网，且落在离网4米的位置，则球拍击打的高度h为（ ）
A、1.0 B、1.6 C、2.0 D、2.44. 如图，在△ABC中，点D在BC边上，连接AD，点G在线段AD上，GE∥BD，且交AB于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是（ ）
A、 B、 C、 D、5. 如图，在 中，点D，E分别为AB，AC边上的点，且 ，CD、BE相较于点O，连接AO并延长交DE于点G，交BC边于点F，则下列结论中一定正确的是（ ）
A、 B、 C、 D、6. 如图，在▱ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则DF的长为（ ）
A、 B、 C、 D、7. 如图，在平行四边形中，点E是边AD的中点．EC交对角线BD于F则EF，则EF：FC等于（ ）
A、1：1 B、1：2 C、3：2 D、3：178. 如图，AB与CD相交于点E，AD∥BC， ，CD=16，则DE的长为（ ）
A、3 B、6 C、 D、109. 如图，已知矩形ABCD，AB=4，AD=2，E为AB的中点，连接DE与AC交于点F，则CF的长等于（ ）
A、 B、 C、 D、二、填空题
-
10. 如图， ，DE=2AE，CF=2BF，且DC=5，AB=8，则EF= ．
11. 如图所示，在 中，AD是高， ，EF=3，BC=5，AD=6，则GD= ．
12. 如图28-1-1-1所示，某斜坡AB上有一点B′，B′C′、BC是边AC上的高，则图中相似的三角形是 ， 则B′C′∶AB′= ， B′C′∶AC′=.
13. 如图，G为△ABC的重心，若EF过点G，且EF∥BC，交AB，AC于E，F，则 ＝ ．
14. 在 中， ， ，AD：BD=5：3，CF=6，则DE的长为 ．
15. 在 中， 分别交AB，AC于点M，N；若AM=1，MB=2，BC=3，则MN的长为 ．
16. 如图，D，E分别为AB的三等分点，DF // EG // B，若BC=12，则DF= ， EG= ．
17. 如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=m．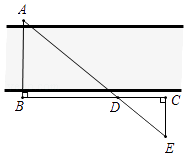
三、解答题
-
18. 已知：如图，四边形ABCD是平行四边形，F是AB上一点，连接DF并延长交CB的延长线于E.
求证：AD：AF＝CE：AB
19. 如图，小强和小华共同站在路灯下，小强的身高EF=1.8m，小华的身高MN=1.5m，他们的影子恰巧等于自己的身高，即BF=1.8m，CN=1.5m，且两人相距4.7m，求路灯AD的高度是多少？
20. 如图，大刚在晚上由灯柱A走向灯柱B，当他走到M点时，发觉他身后影子的顶部刚好接触到灯柱A的底部，当他向前再走12米到N点时，发觉他身前的影子刚好接触到灯柱B的底部，已知大刚的身高是1.6米，两根灯柱的高度都是9.6米，设AM=NB=x米．求：两根灯柱之间的距离．
21. 如图，为了测量河宽，小华采用的办法是：在河的对岸选取一点A，在河的这岸选一点B，使AB与河的边缘垂直，然后在AB的延长线上取一点C，并量得BC=30米；在河的这边取一点D，并量得BD=20米；最后在射线AD上取一点E，使得 ，并量得DE=40米．小华这种做法，她能根据已有的数据求出河宽AB吗？若能，请求出河宽AB；若不能，她还必须测量哪一条线段的长？假设这条线段的长是m米，请你用含m的代数式表示河宽AB．
