2018-2019学年数学华师大版九年级上册23.3.3 相似三角形的性质 同步练习
试卷更新日期:2018-11-16 类型:同步测试
一、选择题
-
1. 已知△ABC∽△DEF,且相似比为2∶1,若△ABC的周长是8 cm,则△DEF的周长是( )A、2 cm B、4 cm C、8 cm D、16 cm2. 已知△ABC∽△DEF,且S△ABC:S△DEF=2:1,则AB与DE的比是( )A、1:2 B、2:1 C、 :1 D、1:3. 已知两个相似三角形的对应边长分别为9cm和11cm,它们的周长相差20cm,则这两个三角形的周长分别为( )A、45cm,65cm B、90cm,110cm C、45cm,55cm D、70cm,90cm4. 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形 (图中阴影部分)的面积分别是4,9和49,则△ABC的面积是( )
 A、81 B、121 C、124 D、1445. 如图, , 、 分别是 的高和中线, 、 分别是 的高和中线,且 , , ,则 的长为( )
A、81 B、121 C、124 D、1445. 如图, , 、 分别是 的高和中线, 、 分别是 的高和中线,且 , , ,则 的长为( ) A、 B、 C、 D、6. 如图,在▱ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2 , 则S△AOB等于( )
A、 B、 C、 D、6. 如图,在▱ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2 , 则S△AOB等于( ) A、24cm2 B、36cm2 C、48cm2 D、60cm27. 已知△ABC∽△DEF,△ABC的长为3,△DEF的周长为1,则△DEF与△ABC的面积之比为( )A、9:1 B、1:9 C、3:1 D、1:38. 如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )
A、24cm2 B、36cm2 C、48cm2 D、60cm27. 已知△ABC∽△DEF,△ABC的长为3,△DEF的周长为1,则△DEF与△ABC的面积之比为( )A、9:1 B、1:9 C、3:1 D、1:38. 如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )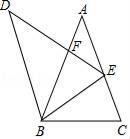 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 两个三角形相似,相似比是 ,如果小三角形的面积是9,那么大三角形的面积是.10. 如图,线段AC与BD相交于点O, ,若OA∶OC=4∶3, 的面积是2,则 的面积等于 .
 11. 已知△ABC∽△DEF, 与 的相似比为4:1,则 与 对应边上的高之比为 .12. 若△ABC∽△A′B′C′,AB=4,BC=5,AC=6,△A′B′C′的最大边长为15,那么它们的相似比是 , △A′B′C′的周长是 .13. 已知△ABC~△DEF, BC边上的高与EF边上的高之比为2:3,则△ABC与△DEF的面积的比为.14. 如图D、E、F分别在△ABC的三边上,BD= AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是.
11. 已知△ABC∽△DEF, 与 的相似比为4:1,则 与 对应边上的高之比为 .12. 若△ABC∽△A′B′C′,AB=4,BC=5,AC=6,△A′B′C′的最大边长为15,那么它们的相似比是 , △A′B′C′的周长是 .13. 已知△ABC~△DEF, BC边上的高与EF边上的高之比为2:3,则△ABC与△DEF的面积的比为.14. 如图D、E、F分别在△ABC的三边上,BD= AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是. 15. 如图,梯形 中, , ,点 在 边上, , , ,若 与 相似,则 的长为 .
15. 如图,梯形 中, , ,点 在 边上, , , ,若 与 相似,则 的长为 .
三、解答题
-
16. 如图,若 , 和 相交于点 ,和 相交于点 , , , ,求 .
 17. 已知:如图,四边形ABCD是平行四边形,F是AB上一点,连接DF并延长交CB的延长线于E.
17. 已知:如图,四边形ABCD是平行四边形,F是AB上一点,连接DF并延长交CB的延长线于E.
求证:AD:AF=CE:AB
18. 如图,已知 中, , , ,点 、 分别在 、 上,如果以 、 、 为顶点的三角形和 相似,且相似比为 ,试求 、 的长. 19. 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
19. 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC. (1)、求证:△ABD∽△DCB;(2)、若AB=12,AD=8,CD=15,求DB的长.
(1)、求证:△ABD∽△DCB;(2)、若AB=12,AD=8,CD=15,求DB的长.

