2018-2019学年数学华师大版九年级上册23.3.2 相似三角形的判定（3） 同步练习
试卷更新日期：2018-11-16 类型：同步测试
一、选择题
-
1. 如图，若果∠1=∠2，那么添加下列任何一个条件：
（1） = ，（2） = ， （3）∠B=∠D，（4）∠C=∠AED，其中能判定△ABC∽△ADE的个数为（ ）
A、1 B、2 C、3 D、42. 在△ABC和△DEF中，∠A=40°，∠D=60°，∠E=80°， ，那么∠B的度数是（ ）A、40° B、60° C、80° D、100°3. 下列条件不能判定△ADB∽△ABC的是（ ）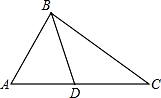
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =4. 下列各组条件中，一定能推得△ABC与△DEF相似的是（ ）A、∠A=∠E且∠D=∠F B、∠A=∠B且∠D=∠F C、∠A=∠E且 D、∠A=∠E且5. 下列说法正确的是（ ）A、对角线相等且互相平分的四边形是菱形 B、对角线垂直且相等的四边形是正方形 C、两角分别相等的两个三角形相似 D、两边成比例且一角相等的两个三角形相似6.如图，在△ABC与△ADE中，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中的（ ）
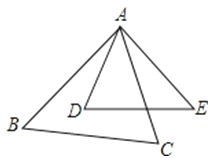A、= B、= C、= D、=7. 如图，∠A=∠B=90°，AB=7，AD=2，BC=3，在边AB上取点P，使得△PAD与△PBC相似，则这样的P点共有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
8. 已知：△ABC中，点E是AB边的中点，点F在AC边上，若以A，E，F为顶点的三角形与△ABC相似，则需要增加的一个条件是 ． （写出一个即可）
9. 如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC=3AD，AB=3AE，点F为BC边上一点，添加一个条件： ， 可以使得△FDB与△ADE相似．（只需写出一个）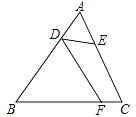
10. 如图标记了△ABC与△DEF边、角的一些数据，如果再添加一个条件使△ABC∽△DEF，那么这个条件可以是 ． （只填一个即可）
11. 如图，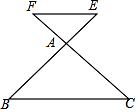
(1)、若AE：AB= ， 则△ABC∽△AEF；(2)、若∠E= ， 则△ABC∽△AEF．12. 如图，在△ABC中，D、E分别为边AB、AC上的点． = ，点F为BC边上一点，添加一个条件： ， 可以使得△FDB与△ADE相似．（只需写出一个）
13. 如图，△ABC中，点D、E分别是AB、AC边上的点，欲使△ADE∽△ACB，则需添加的一个条件是 ． （只写一种情况即可）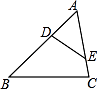
14. 如图，点D为△ABC外一点，AD与BC边的交点为E，AE=3，DE=5，BE=4，要使△BDE∽△ACE，且点B，D的对应点为A，C，那么线段CE的长应等于 ．
三、解答题
-
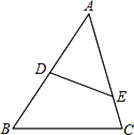
15. 如图，在△ABC中，D、E分别在AB与AC上，且AD=5，DB=7，AE=6，EC=4．
求证：△ADE∽△ACB．
16. 如图所示，点D在△ABC的AB边上，AD=2，BD=4，AC=2 ．求证：△ACD∽△ABC．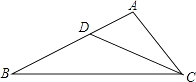
17. 如图，在△ABC中，AB=AC=1，BC= ，在AC边上截取AD=BC，连接BD．
(1)、通过计算，判断AD2与AC•CD的大小关系；
(2)、求∠ABD的度数．
