河北省沧州渤海新区2018—2019学年九年级数学下册综合测试卷
试卷更新日期:2018-11-16 类型:期末考试
一、单选题
-
1. 下列各式中不是反比例函数关系的是( )A、 B、 C、 (a为常量且 ) D、2. 如图,将 沿 边上的中线 平移到 的位置,已知 的面积为9,阴影部分三角形的面积为4.若 ,则 等于( )
 A、2 B、3 C、 D、3. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
A、2 B、3 C、 D、3. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )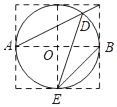 A、 B、 C、2 D、4. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A、 B、 C、2 D、4. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )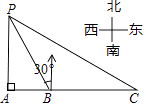 A、40海里 B、60海里 C、20 海里 D、40 海里5. 如图,∠AOB=90°,且OA,OB分别与反比例函数y= (x>0)、y=﹣ (x<0)的图象交于A,B两点,则tan∠OAB的值是( )
A、40海里 B、60海里 C、20 海里 D、40 海里5. 如图,∠AOB=90°,且OA,OB分别与反比例函数y= (x>0)、y=﹣ (x<0)的图象交于A,B两点,则tan∠OAB的值是( ) A、 B、 C、1 D、6. 如图, 经过位似变换得到 ,点 是位似中心且 ,则 与 的面积比是( )
A、 B、 C、1 D、6. 如图, 经过位似变换得到 ,点 是位似中心且 ,则 与 的面积比是( ) A、1:6 B、1:5 C、1:4 D、1:27. 如图,在菱形ABCD中,对角线AC、BD相交于点0,BD=8,tan∠ABD= ,则线段AB的长为( ).
A、1:6 B、1:5 C、1:4 D、1:27. 如图,在菱形ABCD中,对角线AC、BD相交于点0,BD=8,tan∠ABD= ,则线段AB的长为( ). A、 B、2 C、5 D、108. 下列几何体中,主视图与俯视图不相同的是( )
A、 B、2 C、5 D、108. 下列几何体中,主视图与俯视图不相同的是( )
A、正方体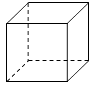 B、四棱锥
B、四棱锥  C、圆柱
C、圆柱  D、球
D、球  9. 如图,已知双曲线y= (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
9. 如图,已知双曲线y= (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )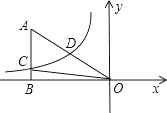 A、12 B、9 C、6 D、410. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2018B2018C2018D2018的边长是( )
A、12 B、9 C、6 D、410. 一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2018B2018C2018D2018的边长是( )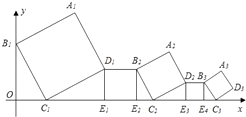 A、( )2017 B、( )2016 C、( )2017 D、( )2016
A、( )2017 B、( )2016 C、( )2017 D、( )2016二、填空题
-
11. 下图是某天内,电线杆在不同时刻的影长,按先后顺序应当排列为 .
 12. 如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为米.(结果保留两个有效数字)【参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601】
12. 如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为米.(结果保留两个有效数字)【参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601】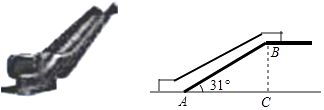 13. 如图中两三角形相似,则x= .
13. 如图中两三角形相似,则x= .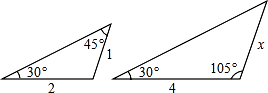 14. 如图,直线l1∥l2∥l3 , 直线AC交l1 , l2 , l3 , 于点A,B,C;直线DF交l1 , l2 , l3于点D,E,F,已知 ,则 =。
14. 如图,直线l1∥l2∥l3 , 直线AC交l1 , l2 , l3 , 于点A,B,C;直线DF交l1 , l2 , l3于点D,E,F,已知 ,则 =。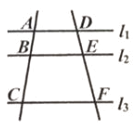 15. 已知A(﹣4, )、B(﹣1, )是反比例函数 图像上的两个点,则 与 的大小关系为 .16. 如图,矩形ABCD中,AB=2 ,AD=6,P为边AD上一点,且AP=2,在对角线BD上寻找一点M,使AM+PM最小,则AM+PM的最小值为 .
15. 已知A(﹣4, )、B(﹣1, )是反比例函数 图像上的两个点,则 与 的大小关系为 .16. 如图,矩形ABCD中,AB=2 ,AD=6,P为边AD上一点,且AP=2,在对角线BD上寻找一点M,使AM+PM最小,则AM+PM的最小值为 . 17. 如图.一艘渔船正以60海里/小时的速度向正东方向航行,在 处测得岛礁 在东北方向上,继续航行1.5小时后到达 处此时测得岛礁 在北偏东 方向,同时测得岛礁 正东方向上的避风港 在北偏东 方向为了在台风到来之前用最短时间到达 处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达 (结果保留根号)
17. 如图.一艘渔船正以60海里/小时的速度向正东方向航行,在 处测得岛礁 在东北方向上,继续航行1.5小时后到达 处此时测得岛礁 在北偏东 方向,同时测得岛礁 正东方向上的避风港 在北偏东 方向为了在台风到来之前用最短时间到达 处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达 (结果保留根号) 18. 如图,把三角形纸片折叠,使点 、点 都与点 重合,折痕分别为 , ,得到 ,若 厘米,则 的边 的长为厘米.
18. 如图,把三角形纸片折叠,使点 、点 都与点 重合,折痕分别为 , ,得到 ,若 厘米,则 的边 的长为厘米. 19. 如图, 中, , , ,将 绕点 顺时针旋转 得到 , 为线段 上的动点,以点 为圆心, 长为半径作 ,当 与 的边相切时, 的半径为.
19. 如图, 中, , , ,将 绕点 顺时针旋转 得到 , 为线段 上的动点,以点 为圆心, 长为半径作 ,当 与 的边相切时, 的半径为. 20. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点B,若 ,则 的值为.
20. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点B,若 ,则 的值为.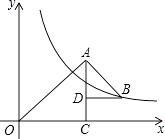
三、解答题
-
21.
一个长方体的三视图如图所示.若其俯视图为正方形,求这个长方体的表面积.
 22. 京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
22. 京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).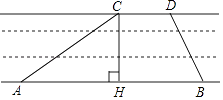 23. 如图双曲线 与矩形 AOCB 的边 AB 、 BC 分别交于 E 、 F 点, OA 、 OC 在坐标轴上,BE=2AE 且S四边形OEBF=2,求 k .
23. 如图双曲线 与矩形 AOCB 的边 AB 、 BC 分别交于 E 、 F 点, OA 、 OC 在坐标轴上,BE=2AE 且S四边形OEBF=2,求 k . 24. 如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.
24. 如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似. 25. 某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
25. 某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:销售量n(件)
n=50﹣x
销售单价m(元/件)
当1≤x≤20时,
当21≤x≤30时,
(1)、请计算第15天该商品单价为多少元/件?(2)、求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)、这30天中第几天获得的利润最大?最大利润是多少?26. 如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设 。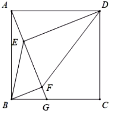 (1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.
(1)、求证:AE=BF;(2)、连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)、设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2 , 求 的最大值.