湖北省荆门市2018--2019学年九年级上学期数学期末测试卷

试卷更新日期：2018-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{4} \cdot a^{3} = a^{12}$ B、 $\sqrt{9} = 3$ C、 ${(x^{2} + 1)}^{0} = 0$ D、若 $x^{2} = x$ ，则x=1

查看试题解析
2. 已知x₁ ， x₂是关于x的方程x²+bx﹣3=0的两根，且满足x₁+x₂﹣3x₁x₂=5，那么b的值为（）

A、4 B、﹣4 C、3 D、﹣3

查看试题解析
3. 如图，在△ABC中，AB=8，AC=6，∠BAC=30°，将△ABC绕点A逆时针旋转60°得到△AB₁C₁ ，连接BC₁ ，则BC₁的长为（）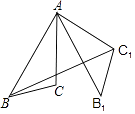

A、6 B、8 C、10 D、12

查看试题解析
4. 下列说法正确的是（）

A、“打开电视机，正在播放体育节目”是必然事件 B、了解夏季冷饮市场上冰淇淋的质量情况适合用普查 C、抛掷一枚普通硬币，“这枚硬币正面朝上”，这一事件发生的概率为 $\frac{1}{2}$ D、甲、乙两人在相同条件下各射击10次，他们的成绩的平均数相同，方差分别是S_甲²=0.3，S_乙²=0.5，则乙的射击成绩较稳定

查看试题解析
5. 下列图形中，既是中心对称图形又是轴对称图形的有 $($ 　　 $)$

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 在一次酒会上，每两人都只碰一次杯，如果一共碰杯55次，则参加酒会的人数为（）

A、9人 B、10人 C、11人 D、12人

查看试题解析
7. 将抛物线y=x²向左平移2个单位，再向下平移5个单位，平移后所得新抛物线的表达式为（）

A、y=（x+2）²﹣5 B、y=（x+2）²+5 C、y=（x﹣2）²﹣5 D、y=（x﹣2）²+5

查看试题解析
8. 规定：如果关于x的一元二次方程ax²+bx+c=0（a≠0）有两个实数根，且其中一个根是另一个根的2倍，则称这样的方程为“倍根方程”．现有下列结论：
①方程x²+2x﹣8=0是倍根方程；

②若关于x的方程x²+ax+2=0是倍根方程，则a=±3；

③若关于x的方程ax²﹣6ax+c=0（a≠0）是倍根方程，则抛物线y=ax²﹣6ax+c与x轴的公共点的坐标是（2，0）和（4，0）；

④若点（m，n）在反比例函数y= $\frac{4}{x}$ 的图象上，则关于x的方程mx²+5x+n=0是倍根方程．

上述结论中正确的有（）

A、①② B、③④ C、②③ D、②④

查看试题解析
9. 如图，在△ABC中，∠ACB=90°，过B，C两点的⊙O交AC于点D，交AB于点E，连接EO并延长交⊙O于点F.连接BF，CF.若∠EDC=135°，CF= $2 \sqrt{2}$ ，则AE²+BE²的值为（）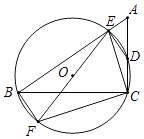

A、8 B、12 C、16 D、20

查看试题解析
10. 在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax²﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）

A、a≤﹣1或 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ B、 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ C、a≤ $\frac{1}{4}$ 或a＞ $\frac{1}{3}$ D、a≤﹣1或a≥ $\frac{1}{4}$

查看试题解析
11. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，下列结论：①2a+b<0；②abc>0；③4a−2b+c>0；④a+c>0，其中正确结论的个数为（）

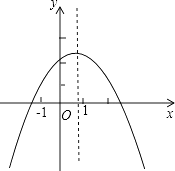A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，抛物线y= $\frac{1}{4}$ （x+2）（x﹣8）与x轴交于A，B两点，与y轴交于点C，顶点为M，以AB为直径作⊙D．下列结论：①抛物线的对称轴是直线x=3；②⊙D的面积为16π；③抛物线上存在点E，使四边形ACED为平行四边形；④直线CM与⊙D相切．其中正确结论的个数是（）

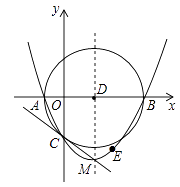A、1 B、2 C、3 D、4

查看试题解析

二、填空题

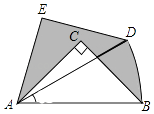
13. 已知α，β是方程x²﹣3x﹣4=0的两个实数根，则α²+αβ﹣3α的值为．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路径为弧BD，则图中阴影部分的面积为．

查看试题解析
15. 某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（不包括门）总长为27m，则能建成的饲养室面积最大为 m² ．

查看试题解析
16.
如图，正方形ABCD的边长为4，E、F分别是BC、CD上的两个动点，且AE⊥EF．则AF的最小值是．

查看试题解析
17.
如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=3 $\sqrt{3}$ ，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE= $\frac{9}{2}$ CE；④S_阴影= $\frac{\sqrt{3}}{2}$ ．其中正确结论的序号是．

查看试题解析

三、计算题

18. 解方程：x²﹣4x+1=0．

查看试题解析
19. 先化简，再求值：（x﹣1）÷（ $\frac{2}{x + 1}$ ﹣1），其中x为方程x²+3x+2=0的根．

查看试题解析

四、解答题

20.
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，其中点A（5，4），B（1，3），将△AOB绕点O逆时针旋转90°后得到△A₁OB₁ ．
（1）画出△A₁OB₁；
（2）在旋转过程中点B所经过的路径长为；
（3）求在旋转过程中线段AB、BO扫过的图形的面积之和．

查看试题解析
21.
某电视台为了了解本地区电视节目的收视率情况，对部分观众开展了“你最喜爱的电视节目”的问卷调查（每人只填写一项），根据收集的数据绘制了下面两幅不完整的统计图．根据要求回答下列问题：
（1）本次问卷调查共调查了多少名观众？
（2）补全图1中的条形统计图；并求出图2中收看“综艺节目”的人数占调查总人数的百分比；
（3）求出图2中“科普节目”在扇形图中所对应的圆心角的度数；
（4）现有喜欢“新闻节目”（记为A）、“体育节目”（记为B）、“综艺节目”（记为C）、“科普节目”（记为D）的观众各一名，电视台要从四人中随机抽取两人参加联谊活动，请用“列表法”或“画树形图”的方法求出恰好抽到喜欢“新闻节目”和“体育节目”两位观众的概率．

查看试题解析
22.
如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．
（1）求证：BE与⊙O相切；
（2）设OE交⊙O于点F，若DF=1，BC=2 $\sqrt{3}$ ，求由劣弧BC、线段CE和BE所围成的图形面积S．

查看试题解析
23. 在2014年巴西世界杯足球赛前夕，某体育用品店购进一批单价为40元的球服，如果按单价60元销售，那么一个月内可售出240套．根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高5元，销售量相应减少20套．设销售单价为x（x≥60）元，销售量为y套．
（1）求出y与x的函数关系式．
（2）当销售单价为多少元时，月销售额为14000元；
（3）当销售单价为多少元时，才能在一个月内获得最大利润？最大利润是多少？
[参考公式：抛物线y=ax²+bx+c（a≠0）的顶点坐标是( $- \frac{b}{2 a}$ , $\frac{4 a c - b^{2}}{4 a}$ )]．

查看试题解析
24.
如图，抛物线y=ax²+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，对称轴与抛物线相交于点P、与直线BC相交于点M，连接PB．
（1）求该抛物线的解析式；
（2）抛物线上是否存在一点Q，使△QMB与△PMB的面积相等？若存在，求点Q的坐标；若不存在，说明理由；
（3）在第一象限、对称轴右侧的抛物线上是否存在一点R，使△RPM与△RMB的面积相等？若存在，直接写出点R的坐标；若不存在，说明理由．

查看试题解析