2019年高考理科数学模拟试卷(全国I卷)
试卷更新日期:2018-11-16 类型:高考模拟
一、单选题
-
1. 设复数 满足 ,则 ( )A、2 B、 C、 D、12. 已知集合 ,则 ( )
A、 或 B、 或 C、 D、3. 是今年国庆中秋长假期间某客运站客运量比去年同期增减情况的条形图.根据图中的信息,以下结论中不正确的是( )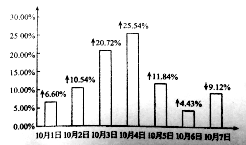 A、总体上,今年国庆长假期间客运站的客流比去年有所增长 B、10月3日、4日的客流量比去年增长较多 C、10月6日的客运量最小 D、10月7日,同比去年客流量有所下滑4. 设等差数列 的前 项和为 .若 , ,则 ( )A、 B、 C、 D、5. 已知函数f(x)=2f(2﹣x)﹣x2+5x﹣5,则曲线y=f(x)在点(1,f(1))处的切线方程为( )A、y=x B、y=﹣2x+3 C、y=﹣3x+4 D、y=x﹣26. 设D为△ABC中BC边上的中点,且O为AD边上靠近点A的三等分点,则( )A、 B、 C、 D、7. 已知四棱锥 的三视图如图所示,则四棱锥 的五个面中面积的最大值是( )
A、总体上,今年国庆长假期间客运站的客流比去年有所增长 B、10月3日、4日的客流量比去年增长较多 C、10月6日的客运量最小 D、10月7日,同比去年客流量有所下滑4. 设等差数列 的前 项和为 .若 , ,则 ( )A、 B、 C、 D、5. 已知函数f(x)=2f(2﹣x)﹣x2+5x﹣5,则曲线y=f(x)在点(1,f(1))处的切线方程为( )A、y=x B、y=﹣2x+3 C、y=﹣3x+4 D、y=x﹣26. 设D为△ABC中BC边上的中点,且O为AD边上靠近点A的三等分点,则( )A、 B、 C、 D、7. 已知四棱锥 的三视图如图所示,则四棱锥 的五个面中面积的最大值是( )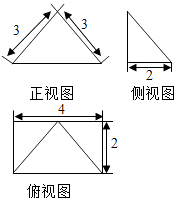 A、3 B、6 C、8 D、108. 设抛物线C的方程为=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=( )
A、3 B、6 C、8 D、108. 设抛物线C的方程为=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=( )
A、 B、- C、 D、-9. 设 是同一个半径为 的球的球面上四点, 为等边三角形且其面积为 ,则三棱锥 体积的最大值为( )A、 B、 C、 D、10. 已知定义在 上的函数 满足 ,且 是偶函数,当 时, .令 ,若在区间 内,函数 有4个不相等实根,则实数 的取值范围是( )A、 B、 C、 D、11. 2018年行平昌冬季奥运会与2月9~2月25日举行,为了解奥运会五环所占面积与单独五个环面积和的比例P,某学生设计了如下的计算机模拟,通过计算机模拟项长为8,宽为5的长方形内随机取了N个点,经统计落入五环及其内部的点数为 个,圆环半径为1,则比值 的近似值为( )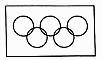 A、 B、 C、 D、12. 过双曲线 的左焦点 作直线交双曲线的两条渐近线于 , 两点,若 为线段 的中点,且 ,则双曲线的离心率为( )A、 B、 C、 D、
A、 B、 C、 D、12. 过双曲线 的左焦点 作直线交双曲线的两条渐近线于 , 两点,若 为线段 的中点,且 ,则双曲线的离心率为( )A、 B、 C、 D、二、填空题
-
13. 若x,y满足约束条件 ,则z=3x﹣4y的最小值为14. 数列{an}中,a1=1,当n≥2时, ,则an= .
15. 某校开设A类选修课4门,B类选修课2门,每位同学需从两类选修课中共选4门,若要求至少选一门B类课程,则不同的选法共有种.(用数字作答)16. 设当x=θ时,函数f(x)=sinx﹣2cosx取得最大值,则cosθ= .三、解答题
-
17. 如图,在平面四边形 中, .
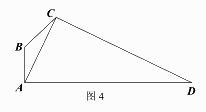
(Ⅰ)若 ,求 ;
(Ⅱ)若 ,求 .
18. 某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表:A型车挖掘机
出租天数
1
2
3
4
5
6
7
车辆数
5
10
30
35
15
3
2
B型车挖掘机
出租天数
1
2
3
4
5
6
7
车辆数
14
20
20
16
15
10
5
(Ⅰ)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(Ⅱ)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
19. 如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC, ,AB⊥AC,D是棱BB1的中点.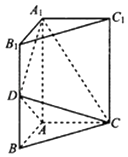
(Ⅰ)证明:平面A1DC⊥平面ADC;
(Ⅱ)求平面A1DC与平面ABC所成二面角的余弦值.
20. 平面直角坐标系xOy中,已知椭圆 的左焦点为F,离心率为 ,过点F且垂直于长轴的弦长为 .(I)求椭圆C的标准方程;
(Ⅱ)设点A,B分别是椭圆的左、右顶点,若过点P(﹣2,0)的直线与椭圆相交于不同两点M,N.
(i)求证:∠AFM=∠BFN;
(ii)求△MNF面积的最大值.
21. 已知f(x)=a(x﹣lnx)+ ,a∈R.(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f′(x)+ 对于任意的x∈[1,2]成立.
四、选考题(请考生在第22、23题中任选一题作答。)