湖北省宜昌市人教版九年级上学期数学《一元二次方程》章节测试卷

试卷更新日期：2018-11-15 类型：单元试卷

进入出卷网下载

一、单选题

1. 将一元二次方程2（x﹣3）=x²+x﹣1化成一般形式后，一次项系数和常数项分别为（）

A、1，﹣4 B、﹣1，5 C、﹣1，﹣5 D、1，﹣6

查看试题解析
2. 关于x的一元二次方程（m﹣2）x²+（2m+1）x+m﹣2=0有两个不相等的正实数根，则m的取值范围是（）

A、m＞ $\frac{3}{4}$ B、m＞ $\frac{3}{4}$ 且m≠2 C、﹣ $\frac{1}{2}$ ＜m＜2 D、 $\frac{3}{4}$ ＜m＜2

查看试题解析
3. 下列方程是关于x的一元二次方程的是（）

A、ax²+bx+c=0 B、x²+ $\frac{1}{x}$ =0 C、2x+c²=0 D、（x﹣2）（3x+1）=x

查看试题解析
4. 关于 $x$ 的一元二次方程 $(a - 2) x^{2} + 2014 x + a^{2} - 4 = 0$ 的一个根是 $0$ ，则 $a$ 的值（）

A、-2 B、2 C、2或-2 D、0

查看试题解析
5. 已知a、b、c分别为Rt△ABC（∠C=90°）的三边的长，则关于x的一元二次方程（c+a）x²+2bx+（c-a）=0根的情况是（　　）.

A、方程无实数根 B、方程有两个不相等的实数根 C、方程有两个相等的实数根 D、无法判断

查看试题解析
6. 关于x的方程（a﹣1）x²+ $\sqrt{a + 1}$ x+2=0是一元二次方程，则a的取值范围是（）

A、a≠1 B、a≥﹣1且a≠1 C、a＞﹣1且a≠1 D、a≠±1

查看试题解析
7. 一元二次方程x²﹣6x+5=0配方后可变形为（）

A、（x﹣3）²=14 B、（x﹣3）²=4 C、（x+3）²=14 D、（x+3）²=4

查看试题解析
8. 用公式法解方程 $x^{2} - 2 = - 3 x$ 时， $a$ ， $b$ ， $c$ 的值依次是（）

A、 $0$ ， $- 2$ ， $- 3$ B、 $1$ ， $3$ ， $- 2$ C、 $1$ ， $- 3$ ， $- 2$ D、 $1$ ， $- 2$ ， $- 3$

查看试题解析
9. 关于x的一元二次方程x²+2（m﹣1）x+m²=0的两个实数根分别为x₁ ， x₂ ，且x₁+x₂＞0，x₁x₂＞0，则m的取值范围是（）

A、m≤ $\frac{1}{2}$ B、m≤ $\frac{1}{2}$ 且m≠0 C、m＜1 D、m＜1且m≠0

查看试题解析
10. 关于 $x$ 的一元二次方程 $k x^{2} + 2 x - 1 = 0$ 有两个不相等实数根，则 $k$ 的取值范围是（）

A、 $k > - 1$ B、 $k \geq - 1$ C、 $k \neq 0$ D、 $k > - 1$ 且 $k \neq 0$

查看试题解析
11. 以3，4为两实数根的一元二次方程为（）

A、 $x^{2} + 7 x + 12 = 0$ B、 $x^{2} - 7 x + 12 = 0$ C、 $x^{2} - 7 x - 12 = 0$ D、 $x^{2} + 7 x - 12 = 0$

查看试题解析
12. 某树主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支总数是43．若设主干长出x个支干，则可列方程（）

A、(x＋1)²＝43 B、x²＋2x＋1＝43 C、x²＋x＋1＝43 D、x(x＋1)＝43

查看试题解析
13. 用配方法解一元二次方程 $x^{2} + 6 x - 16 = 0$ ，把左边写成完全平方形式后结果为（）

A、 ${(x + 3)}^{2} = 25$ B、 $x (x + 6) = 16$ C、 ${(x - 3)}^{2} = 25$ D、 ${(x + 6)}^{2} = 42$

查看试题解析
14. 在某次聚会上，每两人都握了一次手，所有人共握手 $10$ 次，设有 $x$ 人参加这次聚会，则列出方程正确的是（）

A、 $x (x - 1) = 10$ B、 $\frac{x (x - 1)}{2} = 10$ C、 $x (x + 1) = 10$ D、 $\frac{x (x + 1)}{2} = 10$

查看试题解析
15. 已知 $m$ ， $n$ 是关于 $x$ 的一元二次方程 $x^{2} - 3 x + a = 0$ 的两个解，若 $(m - 1) (n - 1) = - 6$ ，则 $a$ 的值为（）

A、 $- 10$ B、 $4$ C、 $- 4$ D、 $10$

查看试题解析

二、解答题

16. 解方程：

(1)、（x+3）²=2x+6；

(2)、x²﹣2x=8．

查看试题解析
17. 已知关于x的一元二次方程2x²－3k+4=0的一个根是1，求k的值和方程的另一根．

查看试题解析
18. 学完一元二次方程后，在一次数学课上，同学们说出了一个方程的特点：
①它的一般形式为ax²+bx+c=0（a、b、c为常数，a≠0）
②它的二次项系数为5
③常数项是二次项系数的倒数的相反数
你能写出一个符合条件的方程吗？

查看试题解析
19. 已知a、b是等腰△ABC的边且满足a²+b²-8a-4b+20=0，求等腰△ABC的周长．

查看试题解析
20. 求证：无论 $k$ 取何值，关于 $x$ 的一元二次方程 $x^{2} - (3 k + 1) x + 2 (k^{2} + k) = 0$ 总有实数根．

查看试题解析
21. 在宽为20m，长为32m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540m² ，求道路的宽．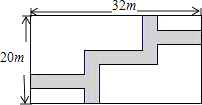

查看试题解析
22. 已知关于 $x$ 的方程 $x^{2} + (m + 2) x + 2 m - 1 = 0$ .

(1)、求证：方程有两个不相等的实数根.

(2)、当 $m$ 为何值时，方程的两根互为相反数？并求出此时方程的解.

查看试题解析
23. 一学校为了绿化校园环境，向某园林公司购买了一批树苗，园林公司规定：如果购买树苗不超过60棵，每棵售价120元；如果购买树苗超过60棵，每增加1棵，所出售的这批树苗每棵售价均降低0.5元，但每棵树苗最低售价不得少于100元，该校最终向园林公司支付树苗款8800元，请问该校共购买了多少棵树苗？

查看试题解析
24.
如图，已知，在直角坐标系xOy中，直线 y= $\frac{4}{3}$ x+8与x轴、y轴分别交于点A、C，点P从A点开始以1个单位/秒的速度沿x轴向右移动，点Q从O点开始以2个单位/秒的速度沿y轴向上移动，如果P、Q两点同时出发，经过几秒钟，能使△PQO的面积为8个平方单位．com

查看试题解析