2016-2017学年云南省昆明市官渡区八年级上学期期末数学试卷
试卷更新日期:2017-03-21 类型:期末考试
一、选择题:
-
1. 分式 有意义的x的取值范围为 .2. 我国医学界最新发现的一种病毒其直径仅为0.000512mm,这个数字用科学记数法可表示为 mm.3. 如图,点E、F、C、B在同一直线上,AB=DE,∠B=∠E,要判定△ABC≌△DEF,还需要添加一个条件,你添加的条件是(写出一个即可)
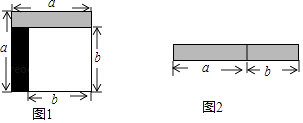
 4. 计算:( )﹣1+(π﹣3)0= .5. 如果一个多边形的内角和是1800°,那么这个多边形的边数是 .6. 已知等腰三角形的一个内角是30°,那么这个等腰三角形顶角的度数是 .7. 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2),上述操作过程能验证的等式是 . (请填入正确答案的序号)
4. 计算:( )﹣1+(π﹣3)0= .5. 如果一个多边形的内角和是1800°,那么这个多边形的边数是 .6. 已知等腰三角形的一个内角是30°,那么这个等腰三角形顶角的度数是 .7. 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2),上述操作过程能验证的等式是 . (请填入正确答案的序号)①a2﹣2ab+b2=(a﹣b)2;
②a2﹣b2=(a+b)(a﹣b);
③a2+ab=a(a+b).
 8. 如图1,某温室屋顶结构外框为△ABC,立柱AD垂直平分横梁BC,∠B=30°,斜梁AC=4m,为增大向阳面的面积,将立柱AD增高并改变位置后变为EF,使屋顶结构外框由△ABC变为△EBC(点E在BA的延长线上)如图2所示,且立柱EF⊥BC,若EF=3m,则斜梁增加部分AE的长为 m.
8. 如图1,某温室屋顶结构外框为△ABC,立柱AD垂直平分横梁BC,∠B=30°,斜梁AC=4m,为增大向阳面的面积,将立柱AD增高并改变位置后变为EF,使屋顶结构外框由△ABC变为△EBC(点E在BA的延长线上)如图2所示,且立柱EF⊥BC,若EF=3m,则斜梁增加部分AE的长为 m.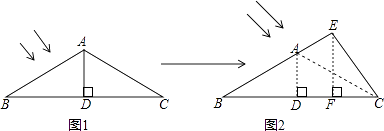
二、选择题:
-
9. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 10. 下列长度的三根木棒能组成三角形的是( )A、3,4,8 B、4,4,8 C、5,6,10 D、6,7,1411. 下列计算中,正确的是( )A、(a2)4=a6 B、a8÷a4=a2 C、(ab2)3=ab6 D、a2•a3=a512. 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
10. 下列长度的三根木棒能组成三角形的是( )A、3,4,8 B、4,4,8 C、5,6,10 D、6,7,1411. 下列计算中,正确的是( )A、(a2)4=a6 B、a8÷a4=a2 C、(ab2)3=ab6 D、a2•a3=a512. 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( ) A、2cm B、3cm C、4cm D、5cm13. 下列分式中最简分式为( )A、 B、 C、 D、14. 如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
A、2cm B、3cm C、4cm D、5cm13. 下列分式中最简分式为( )A、 B、 C、 D、14. 如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( ) A、2对 B、3对 C、4对 D、5对15. 为了响应我市的“绿色家园”行动,某村计划在荒山上种植1200棵树,原计划每天种x棵,由于邻村的支援,每天比原计划多种了40棵,结果提前了5天完成了任务,则可以列出方程为( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =516. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A、2对 B、3对 C、4对 D、5对15. 为了响应我市的“绿色家园”行动,某村计划在荒山上种植1200棵树,原计划每天种x棵,由于邻村的支援,每天比原计划多种了40棵,结果提前了5天完成了任务,则可以列出方程为( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =516. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )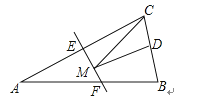 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12三、解答题:
-
17. 计算:(1)、8x2y3•(﹣3xy2)÷6xy;(2)、(x+y)(x﹣2y)+2y(x+y);(3)、(2x+1)2﹣(2x+1)(2x﹣1);(4)、利用乘法公式计算:99×101.18. 因式分解:(1)、3x2﹣75;(2)、x3y﹣4x2y2+4xy3 .19. 在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
 (1)、画出△ABC关于y轴对称的△A1B1C1;(2)、写出点A和对称点A1的坐标;(3)、求出△ABC的面积.20. 如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数.
(1)、画出△ABC关于y轴对称的△A1B1C1;(2)、写出点A和对称点A1的坐标;(3)、求出△ABC的面积.20. 如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数. 21.22. 如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,AB=DE.求证:BE=CF.
21.22. 如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,AB=DE.求证:BE=CF. 23. 先化简,再求值: ÷( +1),其中x=2.24. 从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)、普通列车的行驶路程为千米;(2)、若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.25. 已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
23. 先化简,再求值: ÷( +1),其中x=2.24. 从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)、普通列车的行驶路程为千米;(2)、若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.25. 已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE. (1)、求证:AD=BE;(2)、求∠AEB的度数;(3)、拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)、求证:AD=BE;(2)、求∠AEB的度数;(3)、拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①∠AEB的度数为°;
②探索线段CM、AE、BE之间的数量关系为 . (直接写出答案,不需要说明理由)