河北省2019年中考数学模拟试卷
试卷更新日期:2018-11-15 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 如图为O,A,B,C四点在数线上的位置图,其中O为原点,且AC=1,OA=OB,若C点所表示的数为x,则B点所表示的数与下列何者相等?( )
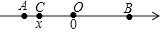 A、﹣(x+1) B、﹣(x﹣1) C、x+1 D、x﹣13. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A、﹣(x+1) B、﹣(x﹣1) C、x+1 D、x﹣13. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )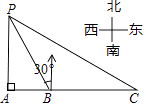 A、40海里 B、60海里 C、20 海里 D、40 海里4. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( )
A、40海里 B、60海里 C、20 海里 D、40 海里4. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( ) A、60° B、75° C、90° D、105°5.
A、60° B、75° C、90° D、105°5.我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
 A、84 B、336 C、510 D、13266. 一组数据2,3,6,8,x的众数是x,其中x是不等式组 的整数解,则这组数据的中位数可能是( )A、3 B、4 C、6 D、3或67.
A、84 B、336 C、510 D、13266. 一组数据2,3,6,8,x的众数是x,其中x是不等式组 的整数解,则这组数据的中位数可能是( )A、3 B、4 C、6 D、3或67.已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax﹣2b与反比例函数y= 在同一平面直角坐标系中的图象大致是( )
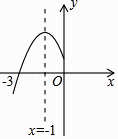 A、
A、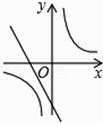 B、
B、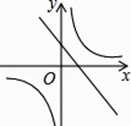 C、
C、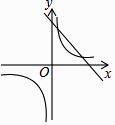 D、
D、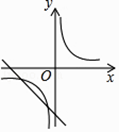 8. 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
8. 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )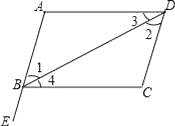 A、∠1=∠2 B、∠3=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°9. 如果m-n=5,那么-3m+3n-7的值是( )
A、∠1=∠2 B、∠3=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°9. 如果m-n=5,那么-3m+3n-7的值是( )
A、22 B、-8 C、8 D、-2210. 如果 ,那么代数式 的值为( )A、 B、 C、 D、11. 某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )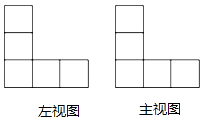 A、4个 B、5个 C、6个 D、7个12. 已知线段AB,下列尺规作图中,PQ与AB的交点O不一定是AB的中点的是( )A、
A、4个 B、5个 C、6个 D、7个12. 已知线段AB,下列尺规作图中,PQ与AB的交点O不一定是AB的中点的是( )A、 B、
B、 C、
C、 D、
D、 13. 下列结论:①两个无理数的和一定是无理数②两个无理数的积一定是无理数③任何一个无理数都能用数轴上的点表示④实数与数轴上的点一一对应,其中正确的是( )
13. 下列结论:①两个无理数的和一定是无理数②两个无理数的积一定是无理数③任何一个无理数都能用数轴上的点表示④实数与数轴上的点一一对应,其中正确的是( )
A、①② B、②③ C、③④ D、②③④14. 下列交通标志图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 15. 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
15. 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )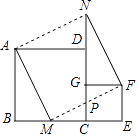 A、2 B、3 C、4 D、516. 规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
A、2 B、3 C、4 D、516. 规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y= 的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A、①② B、③④ C、②③ D、②④二、填空题
-
17. 分解因式:mn2-2mn+m=18. 阅读材料:若ab=N,则b=logaN,称b为以a为底N的对数,例如23=8,则log28=log223=3.根据材料填空:log39= .19. 如图,A,B,C为⊙O上相邻的三个n等分点, ,点E在 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= .
(参考数据:sin15°=cos75°= ,cos15°=sin75°= )

三、解答题
-
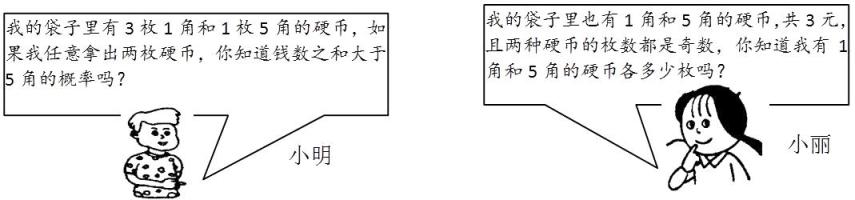
20. 定义新运算:对于任意有理数a,b,都有a⊗b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊗5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5(1)、求(﹣2)⊗3的值;(2)、若4⊗x的值等于13,求x的值.21. 根据小明和小丽的对话解答下列问题:
(小明友情提醒:可借助画树状图或列表的方法,列举所有等可能的结果,再进行计算.小丽友情提醒:情况可不唯一哦.)
 22. 观察下表:
22. 观察下表:序号
1
2
3
…
图形
x x
y
x x
x x x
y y
x x x
y y
x x x
x x x x
y y y
x x x x
y y y
x x x x
y y y
x x x x
…
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)、第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;(2)、若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.①求x,y的值;
②在此条件下,第n个特征多项式是否有最小值?若有,求出最小值和相应的n值.若没有,请说明理由.
23. 为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
(1)观察图象求a,b,m的值
(2)直接写出y1 , y2与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
24. 已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.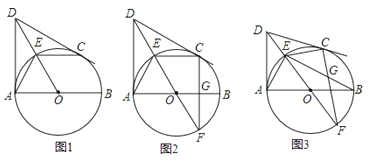
(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE=AD,EF=2 , 求线段CG的长.
25. 如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为多少?
 26. 如图,已知二次函数y=ax2+bx+c(a,b,c为常数)的对称轴为x=1,与y轴的交点为c(0,4),y的最大值为5,顶点为M,过点D(0,1)且平行于x轴的直线与抛物线交于点A,B.
26. 如图,已知二次函数y=ax2+bx+c(a,b,c为常数)的对称轴为x=1,与y轴的交点为c(0,4),y的最大值为5,顶点为M,过点D(0,1)且平行于x轴的直线与抛物线交于点A,B.
(Ⅰ)求该二次函数的解析式和点A、B的坐标;
(Ⅱ)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,求出所有点P的坐标.