2016-2017学年山东省临沂市罗庄区八年级上学期期末数学试卷
试卷更新日期:2017-03-21 类型:期末考试
一、选择题:
-
1. 下列字母或数字具有轴对称性的是( )A、7 B、Z C、1 D、N2. 下列运算结果正确的是( )A、x2+x3=x5 B、x3•x2=x6 C、x5÷x=x5 D、x3•(3x)2=9x53. 若分式 有意义,则a的取值范围是( )A、a≠2 B、a≠0 C、a≠2且a≠0 D、一切实数4. 若(a+b)2=(a﹣b)2+A,则A为( )A、2ab B、﹣2ab C、4ab D、﹣4ab5. 如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )
 A、40° B、30° C、20° D、10°6. 下列各式能用平方差公式分解因式的有( )
A、40° B、30° C、20° D、10°6. 下列各式能用平方差公式分解因式的有( )①x2+y2;②x2﹣y2;③﹣x2﹣y2;④﹣x2+y2;⑤﹣x2+2xy﹣y2 .
A、1个 B、2个 C、3个 D、4个7. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、1个 B、2个 C、3个 D、4个8. 化简(1﹣ )÷ 的结果是( )A、(x+1)2 B、(x﹣1)2 C、 D、9. 如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2 , 则阴影部分面积等于( )
A、1个 B、2个 C、3个 D、4个8. 化简(1﹣ )÷ 的结果是( )A、(x+1)2 B、(x﹣1)2 C、 D、9. 如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2 , 则阴影部分面积等于( ) A、2cm2 B、1cm2 C、 cm2 D、 cm210. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )A、 B、 = C、 D、11. 若3x=15,3y=5,则3x﹣y等于( )A、5 B、3 C、15 D、1012. 已知关于x的分式方程 + =1的解是非负数,则m的取值范围是( )A、m>2 B、m≥2 C、m≥2且m≠3 D、m>2且m≠3
A、2cm2 B、1cm2 C、 cm2 D、 cm210. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )A、 B、 = C、 D、11. 若3x=15,3y=5,则3x﹣y等于( )A、5 B、3 C、15 D、1012. 已知关于x的分式方程 + =1的解是非负数,则m的取值范围是( )A、m>2 B、m≥2 C、m≥2且m≠3 D、m>2且m≠3二、填空题:
-
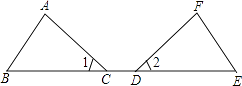
13. 如图,C、D点在BE上,∠1=∠2,BD=EC请补充一个条件: , 使△ABC≌△FED.
 14. 等腰三角形周长为21cm,若有一边长为9cm,则等腰三角形其他两边长为 .15. 若x2﹣mx+4是完全平方式,则m= .16.
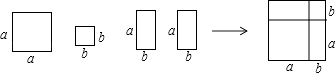
14. 等腰三角形周长为21cm,若有一边长为9cm,则等腰三角形其他两边长为 .15. 若x2﹣mx+4是完全平方式,则m= .16.利用1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式 .
 17. 如图,在直角△ABC中,已知∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且∠ADC=30°,BD=18cm,则AC的长是 cm.
17. 如图,在直角△ABC中,已知∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且∠ADC=30°,BD=18cm,则AC的长是 cm. 18. 若(x﹣y﹣2)2+|xy+3|=0,则( ﹣ )÷ 的值是 .19. 数学家发明了一个魔术盒,当任意数对(a,b)进入其中时,会得到一个新的数:(a﹣1)(b﹣2).现将数对(m,1)放入其中,得到数n,再将数对(n,m)放入其中后,最后得到的数是 . (结果要化简)20. 某快递公司的分拣工小王和小李,在分拣同一类物件时,小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同.已知小王每小时比小李多分拣8个物件,设小李每小时分拣x个物件,根据题意列出的方程是 .
18. 若(x﹣y﹣2)2+|xy+3|=0,则( ﹣ )÷ 的值是 .19. 数学家发明了一个魔术盒,当任意数对(a,b)进入其中时,会得到一个新的数:(a﹣1)(b﹣2).现将数对(m,1)放入其中,得到数n,再将数对(n,m)放入其中后,最后得到的数是 . (结果要化简)20. 某快递公司的分拣工小王和小李,在分拣同一类物件时,小王分拣60个物件所用的时间与小李分拣45个物件所用的时间相同.已知小王每小时比小李多分拣8个物件,设小李每小时分拣x个物件,根据题意列出的方程是 .三、解答题:
-
21. 综合题。(1)、因式分解:a3﹣2a2+a;(2)、因式分解:(3x+y)2﹣(x﹣3y)2;(3)、解方程: =1﹣ .22. 在数学课上,教师对同学们说:“你们任意说出一个x的值(x≠0,1,2),我立刻就知道式子 的计算结果”.请你说出其中的道理.23.
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
 (1)、画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)、在DE上画出点P,使PB+PC最小.24. 如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,CE=1,延长CE、BA交于点F.
(1)、画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)、在DE上画出点P,使PB+PC最小.24. 如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,CE=1,延长CE、BA交于点F. (1)、求证:△ADB≌△AFC;(2)、求BD的长度.25. 在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.(1)、甲、乙两队单独完成建校工程各需多少天?(2)、在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?26.
(1)、求证:△ADB≌△AFC;(2)、求BD的长度.25. 在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.(1)、甲、乙两队单独完成建校工程各需多少天?(2)、在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?26.问题背景:
 (1)、如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
(1)、如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)、如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由;(3)、如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.