北师大版八年级上学期数学期末模拟试卷

试卷更新日期：2018-11-15 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数 0， $\sqrt{3}$ ， $2 π$ ， $\frac{9}{11}$ ，3.14 ，2.3030030003…(相邻两个3之间0的个数逐渐加1)中，其中无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
2. 一组数据5，2，6，9，5，3的众数、中位数、平均数分别是（）

A、5，5，6 B、9，5，5 C、5，5，5 D、2，6，5

查看试题解析
3. 如图，AD⊥CD，CD=4，AD=3，∠ACB=90°，AB=13，则 BC 的长是（）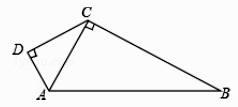

A、8 B、10 C、12 D、16

查看试题解析
4. 为了绿化校园，30名学生共种78棵树苗．其中男生每人种3棵，女生每人种2棵，该班男生有x人，女生有y人．根据题意，所列方程组正确的是（）

A、 ${\begin{matrix} x + y = 78 \\ 3 x + 2 y = 30 \end{matrix}$ B、 ${\begin{matrix} x + y = 78 \\ 2 x + 3 y = 30 \end{matrix}$ C、 ${\begin{matrix} x + y = 30 \\ 2 x + 3 y = 78 \end{matrix}$ D、 ${\begin{matrix} x + y = 30 \\ 3 x + 2 y = 78 \end{matrix}$

查看试题解析
5. 如图，AB∥CD，则图中α，β，γ三者之间的关系是（）

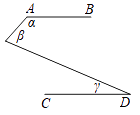A、α+β+γ=180° B、α–β+γ=180° C、α+β–γ=180° D、α+β+γ=360°

查看试题解析
6. 下列函数：①y=7x+1；②y= $\sqrt{5} x$ +2；③y= $\frac{9}{x}$ ﹣5；④y=x，其中属于一次函数的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 已知点A在x轴上，且点A到y轴的距离为4，则点A的坐标为（）

A、(4，0) B、(0，4) C、(4，0)或(－4，0) D、(0，4)或(0，－4)

查看试题解析
8. 一家电信公司提供两种手机的月通话收费方式供用户选择，其中一种有月租费，另一种无月租费．这两种收费方式的通话费用y(元)与通话时间x(min)之间的函数关系如图所示．小红根据图象得出下列结论：①l₁描述的是无月租费的收费方式；②l₂描述的是有月租费的收费方式；③当每月的通话时间为500min时，选择有月租费的收费方式省钱．其中，正确结论的个数是（）

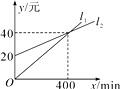A、0 B、1 C、2 D、3

查看试题解析
9. 在平面直角坐标系中，将点P（-2,3）沿X轴方向向右平移3个单位得到点Q,则点Q的坐标是（）

A、(-2,6) B、（-2,0） C、（-5,3 ） D、（1,3）

查看试题解析
10. 由方程组 ${\begin{matrix} x + m = 6 \\ y - m = 3 \end{matrix}$ 可以得出 $x, y$ 的关系式是（）

A、 $x + y = 3$ B、 $x + y = - 3$ C、 $x + y = - 9$ D、 $x + y = 9$

查看试题解析
11. 甲、乙两车沿同一平直公路由A地匀速行驶（中途不停留）前往终点B地，甲、乙两车的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示，小红通过图象得出以下4个信息：①甲车速度为60千米/小时；②A、B两地相距240千米；③乙车行驶2小时追上甲车；④乙车由A地到B地共用3小时．上述信息正确的有（）个．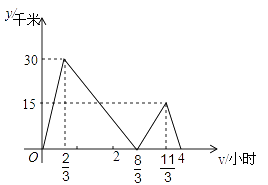

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，在直角坐标系中有线段AB，AB＝50cm，A、B到x轴的距离分别为10cm和40cm，B点到y轴的距离为30cm，现在在x轴、y轴上分别有动点P、Q，当四边形PABQ的周长最短时，则这个值为（　　）

A、50 B、50 $\sqrt{5}$ C、50 $\sqrt{5}$ －50 D、50 $\sqrt{5}$ ＋50

查看试题解析

二、填空题

13. 在一组数据1、0、4、5、8中插入一个数据x，使该组数据的中位数为3，则x=.

查看试题解析
14. 已知点P（a+1，2a-1）关于x轴的对称点在第一象限，则|a+2|-|1-a|= ．

查看试题解析
15. 如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为．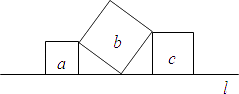

查看试题解析
16. 如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，当 $| B C - A C |$ 最大时，点C的坐标是.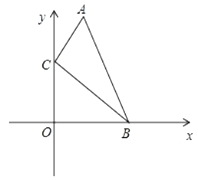

查看试题解析

三、解答题

17. 计算题

(1)、 $\frac{1}{2} \sqrt{16} - \sqrt{4} + (3 - \sqrt{3}) (3 + \sqrt{3})$

(2)、 ${(\sqrt{2} - 2)}^{2} - \frac{6}{\sqrt{2}}$

查看试题解析
18. 甲、乙两人共同解方程组 ${\begin{matrix} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{matrix}$ ，由于甲看错了方程①中的 $a$ ，得到方程组的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ；乙看错了方程②中的 $b^{}$ ，得到方程组的解为 ${\begin{matrix} x = 5 \\ y = 4 \end{matrix}$ ，试计算 $a^{2012} + {(- \frac{1}{10} b)}^{2013}$ 的值.

查看试题解析
19. 在数学、外语、语文3门学科中，某校一年级开展了同学们最喜欢学习哪门学科的调查（一年级共有200人）．
（1）调查的问题是什么？
（2）调查的对象是谁？
（3）在被调查的200名学生中，有40人最喜欢学语文，60人最喜欢学数学，80人最喜欢学外语，其余的人选择其他，求最喜欢学数学这门学科的学生占学生总数的比例；
（4）根据调查情况，把一年级的学生最喜欢学习某学科的人数及其占学生总数的百分比填入下表：

语文
外语
数学
其他
人数

占学生总数的百分比

查看试题解析
20. 如图，△ABC中，AC=BC，点D在BC上，作∠ADF＝∠B，DF交外角∠ACE的平分线CF于点F．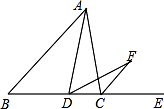

(1)、求证：CF∥AB；

(2)、若∠CAD＝20°，求∠CFD的度数．

查看试题解析
21. 已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．
根据以上信息，解答下列问题：
（1）1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？
（2）请你帮该物流公司设计租车方案；
（3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．

查看试题解析
22. 如图，AB⊥BC，射线CM⊥BC，且BC=4，AB=1，点P是线段BC（不与点
B、C重合）上的动点，过点P作DP⊥AP交射线CM于点D，连结AD．

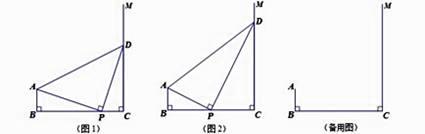(1)、如图1，若BP=3，求△ABP的周长；

(2)、如图2，若DP平分∠ADC，试猜测PB和PC的数量关系，并说明理由；

(3)、若△PDC是等腰三角形，作点B关于AP的对称点B′，连结B′D，则
B′D= ．（请直接写出答案）

查看试题解析
23. 如图，在平面直角坐标系xOy中，一次函数y＝k₁x＋b的图象与x轴交于点A（－3，0），与y轴交于点B，且与正比例函数y＝kx的图象交点为C（3，4）．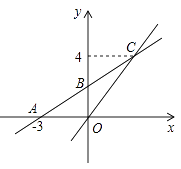

(1)、求正比例函数与一次函数的关系式；

(2)、若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，请求出点D的坐标；

(3)、在x轴上是否存在一点E使△BCE周长最小，若存在，求出点E的坐标

(4)、在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．

查看试题解析

	语文	外语	数学	其他
人数
占学生总数的百分比