天津市宝坻区口东镇2018届九年级上学期数学12月月考试卷

试卷更新日期：2018-11-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $x (x + 3) = x + 3$ 的解是（）

A、 $x = 1$ B、x₁=0，x₂=-3 C、x₁=1，x₂=-3 D、x₁=1， x₂=-37．

查看试题解析
3. 下列条件是随机事件的是（）

A、通常加热到100℃时，水沸腾 B、在只装有黑球和白球的袋子里，摸出红球 C、购买一张彩票，中奖 D、太阳从东方升起

查看试题解析
4. 已知⊙O的半径为5，圆心O到直线 $l$ 的距离为3，则直线 $l$ 与⊙O的位置关系是（）

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
5. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x + 2)}^{2} = 9$ C、 ${(x - 1)}^{2} = 6$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
6. 如图， $P A ， P B$ 分别是⊙O的切线， $A ， B$ 为切点， $A C$ 是⊙O的直径，已知 $∠ B A C = 35^{\circ}$ ， $∠ P$ 的度数为（）

A、 $35^{\circ}$ B、 $45^{\circ}$ C、 $60^{\circ}$ D、 $70^{\circ}$

查看试题解析
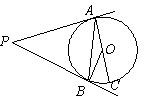7. 若关于x的一元二次方程ax²+x﹣1=0有实数根，则a的取值范围是（）

A、a≥- $\frac{1}{4}$ 且a≠0 B、a≤- $\frac{1}{4}$ C、a≥- $\frac{1}{4}$ D、a≤- $\frac{1}{4}$ 且a≠0

查看试题解析
8. 如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，若把Rt△ABC绕直线AC旋转一周，则所得圆锥的侧面积等于（）

A、6π B、9π C、12π D、15π

查看试题解析
9. 如图，△ABC内接于⊙O，AB=BC，∠ABC=120°，AD为⊙O的直径，AD＝10，那么BD＝（）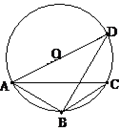

A、8 B、5 C、8 $\sqrt{3}$ D、5 $\sqrt{3}$

查看试题解析
10. 抛物线y=x²﹣2x﹣3的图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=x²+bx+c，则b、c的值为（）

A、b=2，c=2 B、b=2，c=﹣1 C、b=﹣2，c=﹣1 D、b=﹣3，c=2

查看试题解析
11. 初中毕业时，九年级(1)班的每个同学都将自己的相片向全班其他同学各送1张留作纪念，全班共送了2070张相片，如果全班有x名学生，根据题意，列出方程为（）

A、x(x－1)＝2 070 B、x(x＋1)＝2 070 C、2x(x＋1)＝2 070 D、 $\frac{x (x - 1)}{2}$ ＝2 070

查看试题解析
12. 如图，已知顶点为（－3，－6）的抛物线 $y = a x^{2} + b x + c$ 经过点（－1，－4），下列结论：①b²＞4ac；②ax²+bx+c≥－6；③若点（－2，m），（－5，n）在抛物线上，则m＞n；④关于x的一元二次方程 $a x^{2} + b x + c = - 4$ 的两根为﹣5和﹣1，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

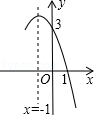
13. 已知A（a，1）与B（5，b）关于原点对称，则a﹣b= ．

查看试题解析
14. 已知关于x方程x²﹣6x+m²﹣2m+5=0的一个根为1，则m²﹣2m= ．

查看试题解析
15. 抛物线y=﹣x²+bx+c的部分图象如图所示，若y＞0，则x的取值范围是．

查看试题解析
16. 如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度AB为24米，拱高CD为8，则拱的半径为。

查看试题解析
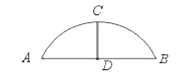17. 在一个不透明的口袋中，装有若干个红球和6个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.3，则估计盒子中大约有红球。

查看试题解析
18. 如图，已知∠APB=30°，OP=3cm，⊙O的半径为1cm，若圆心O沿着BP的方向在直线BP上移动．

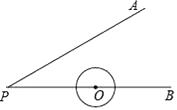(1)、当圆心O移动的距离为1cm时，则⊙O与直线PA的位置关系是．

(2)、若圆心O的移动距离是d，当⊙O与直线PA相交时，则d的取值范围是．

查看试题解析

三、解答题

19. 用适当的方法解下列方程

(1)、x²﹣1=4（x+1）

(2)、3x²﹣6x+2=0．

查看试题解析
20. 如图，已知点A，B的坐标分别为（0，0）、（2，0），将△ABC绕C点按顺时针方向旋转90°得到△A₁B₁C．

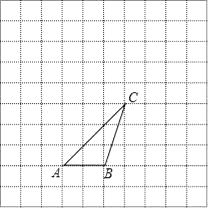(1)、画出△A₁B₁C；

(2)、A的对应点为A₁ ，写出点A₁的坐标；

(3)、求出BB₁的长．（直接作答）

查看试题解析
21. 从同一副扑克牌中拿出黑桃2，3，4，5，背面朝上洗匀后摆在桌面上，从中随机抽取一张（不放回），再从剩下的3张中随机抽取第二张．

(1)、用列表法（或树状图）的方法，列出前后两次抽得的扑克牌上所标数字的所有可能情况；

(2)、计算抽得的两张扑克牌上数字之积为奇数的概率．

查看试题解析
22. 如图，AB为⊙O的直径，点C，D在⊙O上，且BC＝6 cm，AC＝8 cm，∠ABD＝45°.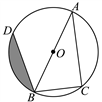

(1)、求BD的长；

(2)、求图中阴影部分的面积．

查看试题解析
23. 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．

(1)、求平均每天销售量 $y$ 箱与销售价 $x$ 元/箱之间的函数关系式．

(2)、当每箱苹果的销售价 $x$ 为多少元时，可以使获得的销售利润w最大？最大利润是多少？

查看试题解析
24. 如图，已知以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为弧BE的中点，连接AD交OE于点F，若AC=FC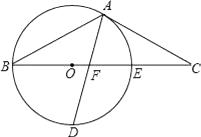
（1）求证：AC是⊙O的切线；
（2）若BF=5，DF= $\sqrt{17}$ ，求⊙O的半径．

查看试题解析
25. 如图，矩形OABC在平面直角坐标系xOy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4，OC=3，若抛物线的顶点在BC边上，且抛物线经过O，A两点，直线AC交抛物线于点D．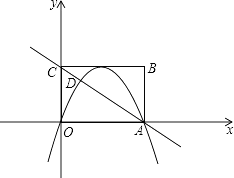

(1)、求抛物线的解析式；

(2)、求点D的坐标；

(3)、若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．

查看试题解析