广东省汕头市潮阳区铜盂镇2017-2018学年八年级上学期数学11月月考试卷
试卷更新日期：2018-11-14 类型：月考试卷
一、单选题
-
1. 下列银行标志中，不是轴对称图形的为（ ）A、
B、
C、
D、
2. 下列运算中，计算结果正确的是 （ ）A、 B、 C、 D、3. 和点P（﹣3，2）关于x轴对称的点是（ ）A、（3，2） B、（﹣3，2） C、（3，﹣2） D、（﹣3，﹣2）4. 等腰三角形的一个角是50°，则它的底角是（ ）A、50° B、65° C、80° D、50°或65°5. 一个多边形的每一个外角都等于36 ，则该多边形的内角和等于（ ）A、1080° B、900° C、1440° D、720°6. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）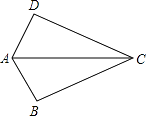
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°7. 如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（ ）
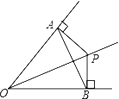A、PA=PB B、PO平分∠APB C、AB垂直平分OP D、OA=OB8. 如图，ΔABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于D，DE⊥AB于E，且AB=6cm， 则ΔDEB的周长为（ ）
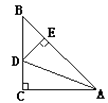A、4cm B、6cm C、10cm D、以上都不对9. 如图，在△ABC中，AB=10，AC=8，则BC边上的中线AD的取值范围是（ ）
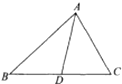A、2＜AD＜18 B、3＜AD＜6 C、4＜AD＜12 D、1＜AD＜9二、填空题
-
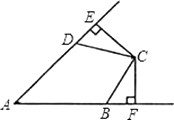
10. 在ΔABC中，AB=AC=3cm，且∠A=60°，则BC的长度为 。11. 已知等腰三角形的两边长分别为x和y，且x和y满足|x﹣5|+（y﹣2）2=0，则这个等腰三角形的周长为 ．12. 如图，D是AB边上的中点，将△ABC沿过D的直线折叠，使点A落在BC上F处，若∠B=50°，则∠BDF= ．
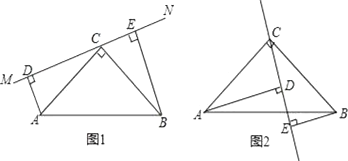
13. 如图，△ABC中，∠ABC=90°，AB=12，BC=5，AC=13，BD⊥AC于D，则BD= ．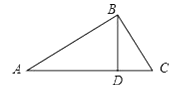
14. 如图，OP平分∠AOB，PD⊥OB于D，∠OPD=60°，PO=4，则点P到边OA的距离是 ．
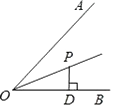15. 如图，在边长为2的等边△ABC中，AD⊥BC于点D，且AD= ，E为AC中点，P为AD上一点则△PEC周长的最小值是 ．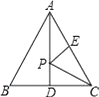
三、解答题
-
16. 计算：
17. 已知点P（2m+1，m-3）关于y轴对称的对称点在第四象限，求m的取值范围。18. 如图，已知△ABC，∠C=90°，AC＜BC，D为BC上一点，且到A，B两点的距离相等．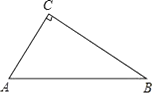
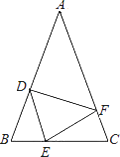
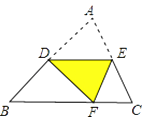
(1)、用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；(2)、连结AD，若∠B=33°，则∠CAD=°．19. 如图，△ABC中，AB=AC，∠A=120°，AB的垂直平分线EF交AB于E，交BC于F。求证：CF=2BF。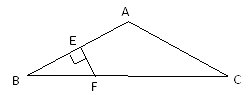
20. 如图，在△ABC中，∠A=60°，∠B=50°， BC边上的垂直平分线DE交BC、AB分别于点D、E，△AEC的周长是13，BC=6。求∠ACE的度数和△ABC的周长。
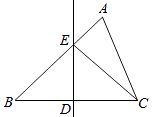21. 如图，点D、B分别在∠A的两边上，C是∠A内一点，且AB=AD，BC=DC，CE⊥AD，CF⊥AB，垂足分别为E、F。求证：CE=CF．
