山东省青岛市2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-11-13 类型：期中考试

进入出卷网下载

一、单选题

1.
如图，在矩形、锐角三角形、正五边形、直角三角形的外边加一个宽度一样的外框，保证外框的边与原图形的对应边平行，则外框与原图一定相似的有（　　）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. △ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a²+b²=c² ，那么下列结论正确的是（　　）

A、bcosB=c B、csinA=a C、atanA=b D、tanB= $\frac{b}{c}$

查看试题解析
3. 利用反证法证明“直角三角形至少有一个锐角不小于45°”，应先假设（　　）

A、直角三角形的每个锐角都小于45° B、直角三角形有一个锐角大于45° C、直角三角形的每个锐角都大于45° D、直角三角形有一个锐角小于45°

查看试题解析
4. 若关于x的一元二次方程2x²﹣3x﹣k=0的一个根为1，则另一个根为（）

A、2 B、﹣1 C、 $\frac{1}{2}$ D、 $\frac{7}{2}$

查看试题解析
5. 如图，□ABCD中，E是AD延长线上一点，BE交AC于点F ，交DC于点G ，则下列结论中错误的是（　　）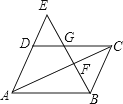

A、△ABE∽△DGE B、△CGB∽△DGE C、△BCF∽△EAF D、△ACD∽△GCF

查看试题解析
6. 用配方法解一元二次方程2x²﹣x﹣1=0时，配方正确的是（）

A、（x﹣ $\frac{1}{4}$ ）²= $\frac{9}{16}$ B、（x+ $\frac{1}{4}$ ）²= $\frac{9}{16}$ C、（x﹣ $\frac{1}{2}$ ）²= $\frac{5}{4}$ D、（x+ $\frac{1}{2}$ ）²= $\frac{5}{4}$

查看试题解析
7. 如图，⊙O过点B，C，圆心O在等腰直角△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为（）

A、 $\sqrt{10}$ B、2 $\sqrt{3}$ C、 $\sqrt{13}$ D、3 $\sqrt{2}$

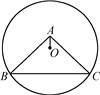查看试题解析
8.
如图，斜面AC的坡度（CD与AD的比）为1：2，AC=3 $\sqrt{5}$ 米，坡顶有旗杆BC，旗杆顶端B点与A点有一条彩带相连．若AB=10米，则旗杆BC的高度为（）

A、5米 B、6米 C、8米 D、（3+ $\sqrt{5}$ ）米

查看试题解析
9. 如图，⊙O△ABC的三条边所得的弦长相等，则下列说法正确的是（）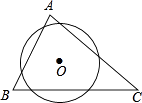

A、点O是△ABC的内心 B、点O是△ABC的外心 C、△ABC是正三角形 D、△ABC是等腰三角形

查看试题解析
10. 关于x的一元二次方程x²﹣ $\sqrt{2}$ x+sinα=0有两个相等的实数根，则锐角α等于（）

A、15° B、30° C、45° D、60°

查看试题解析
11.
如图，四边形BDCE内接于以BC为直径的⊙A，已知：BC=10，cos∠BCD= $\frac{3}{5}$ ， ∠BCE=30°，则线段DE的长是（　　）

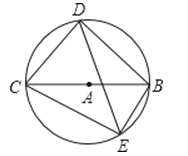A、 $\sqrt{89}$ B、7 $\sqrt{3}$ C、4+3 $\sqrt{3}$ D、3+4 $\sqrt{3}$

查看试题解析
12. 如图，△ABC中，A、B两个顶点在x轴的上方，点C的坐标是（1，0），以点C位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍，设点B的横坐标是a，则点B的对应点B′的横坐标是（）

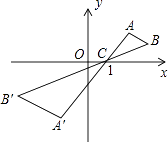A、﹣2a B、2a﹣2 C、3﹣2a D、2a﹣3

查看试题解析
13. 如图，AB是⊙O的直径，PA切⊙O于点A，OP交⊙O于点C，连接BC．若∠P=20°，则∠B的度数是（）

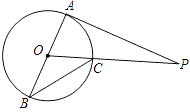A、20° B、25° C、30° D、35°

查看试题解析
14. 如图，在Rt△ABC中，∠C=90°，AC=8，BC=4，分别以AC，BC为直径画半圆，则图中阴影部分的面积为（）

A、10π-8 B、10π-16 C、10π D、5π

查看试题解析
15. 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4 $\sqrt{3}$ 与x轴、y轴分别交于A，B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（）

A、6 B、8 C、10 D、12

查看试题解析
16. 如图，在矩形ABCD中，对角线AC、BD相交于G，E为AD的中点，连接BE交AC于F，连接FD，若∠BFA=90°，则下列四对三角形：①△BEA与△ACD；②△FED与△DEB；③△CFD与△ABG；④△ADF与△EFD，其中相似的为（）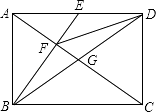

A、①④ B、①② C、②③④ D、①②③④

查看试题解析
17. 你知道吗？股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．已知一支股票某天跌停，之后两天时间又涨回到原价，若这两天此股票股价的平均增长率为x，则x满足的方程是（）

A、（1+x）²= $\frac{11}{10}$ B、x+2x= $\frac{11}{10}$ C、（1+x）²= $\frac{10}{9}$ D、1+2x= $\frac{10}{9}$

查看试题解析
18. 将一副三角板如下图摆放在一起，连接AD，则∠ADB的正切值为（）

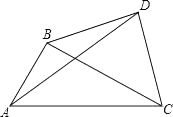A、 $\sqrt{3} - 1$ B、 $\sqrt{3} + 1$ C、 $\frac{\sqrt{3} + 1}{2}$ D、 $\frac{\sqrt{3} - 1}{2}$

查看试题解析
19. 彼此相似的矩形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …，按如图所示的方式放置．点A₁ ， A₂ ， A₃ ， …，和点C₁ ， C₂ ， C₃ ， …，分别在直线y=kx+b（k＞0）和x轴上，已知点B₁、B₂的坐标分别为（1，2），（3，4），则Bn的坐标是（）

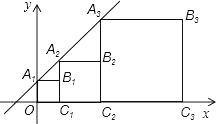A、（2ⁿ﹣1，2ⁿ） B、（2ⁿ﹣ $\frac{1}{2}$ ，2ⁿ） C、（2ⁿ^﹣¹﹣ $\frac{1}{2}$ ，2ⁿ^﹣¹） D、（2ⁿ^﹣¹﹣1，2ⁿ^﹣¹）

查看试题解析
20. 图1是用钢丝制作的一个几何探究工具，其中△ABC内接于⊙G，AB是⊙G的直径，AB=6，AC=2．现将制作的几何探究工具放在平面直角坐标系中（如图2），然后点A在射线OX上由点O开始向右滑动，点B在射线OY上也随之向点O滑动（如图3），当点B滑动至与点O重合时运动结束．在整个运动过程中，点C运动的路程是（）

A、4 B、6 C、4 $\sqrt{2}$ ﹣2 D、10﹣4 $\sqrt{2}$

查看试题解析

二、填空题

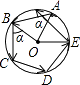
21. 计算： sin²60°+cos²60°﹣tan45°= ．

查看试题解析
22. 一元二次方程（x﹣1）（x﹣2）=x﹣1的解是．

查看试题解析
23. 如图所示，小华从一个圆形场地的A点出发，沿着与半径OA夹角为α的方向行走，走到场地边缘B后，再沿着与半径OB夹角为α的方向折向行走．按照这种方式，小华第五次走到场地边缘时处于弧AB上，此时∠AOE=56°，则α的度数是．

查看试题解析
24. 设△ABC的面积为1，如图①，将边BC、AC分别2等分，BE₁、AD₁相交于点O，△AOB的面积记为S₁；如图②将边BC、AC分别3等分，BE₁、AD₁相交于点O，△AOB的面积记为S₂；…，依此类推，则S_n可表示为．（用含n的代数式表示，其中n为正整数）

查看试题解析

三、解答题

25. 如图，已知：AP²=AQ•AB，且∠ABP=∠C，试说明△QPB∽△PBC．

查看试题解析
26. 某地发生8.1级地震，震源深度20千米．救援队火速赶往灾区救援，探测出某建筑物废墟下方点C处有生命迹象．在废墟一侧某面上选两探测点A、B，AB相距2米，探测线与该面的夹角分别是30°和45°（如图）．试确定生命所在点C与探测面的距离．（参考数据 $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
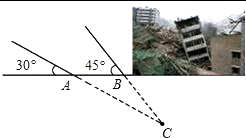27. 为满足市场需求，新生活超市在端午节前夕购进价格为3元/个的某品牌粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个，为了维护消费者利益，物价部门规定，该品牌粽子售价不能超过进价的200%，请你利用所学知识帮助超市给该品牌粽子定价，使超市每天的销售利润为800元．

查看试题解析
28. 如图，等腰三角形ABC中，AC=BC=10，AB=12，以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．

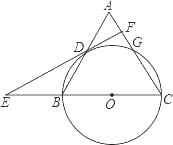(1)、求证：直线EF是⊙O的切线；

(2)、求cos∠E的值．

查看试题解析
29. 在Rt△ABC中，∠BAC=90°，过点B的直线MN∥AC，D为BC边上一点，连接AD，作DE⊥AD交MN于点E，连接AE．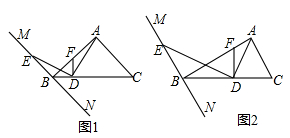

(1)、如图①，当∠ABC=45°时，求证：AD=DE；理由；

(2)、如图②，当∠ABC=30°时，线段AD与DE有何数量关系？并请说明理由；

(3)、当∠ABC=α时，请直接写出线段AD与DE的数量关系．（用含α的三角函数表示）

查看试题解析